1-05 PythonからEXCELに移植してみる
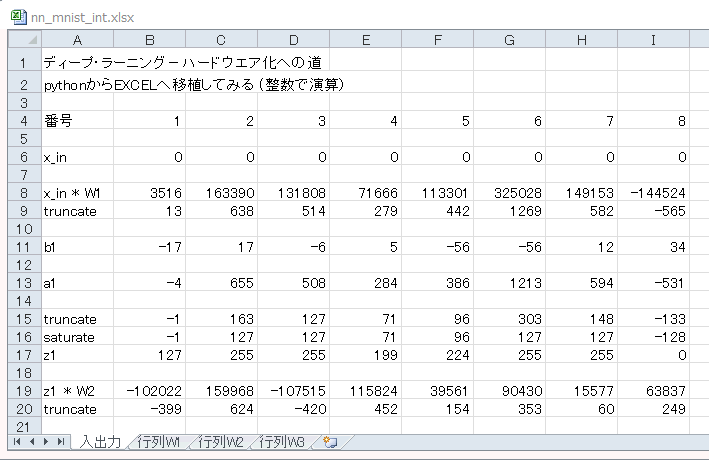 図1-15 EXCEL表の最初のシート。ここで演算を行う
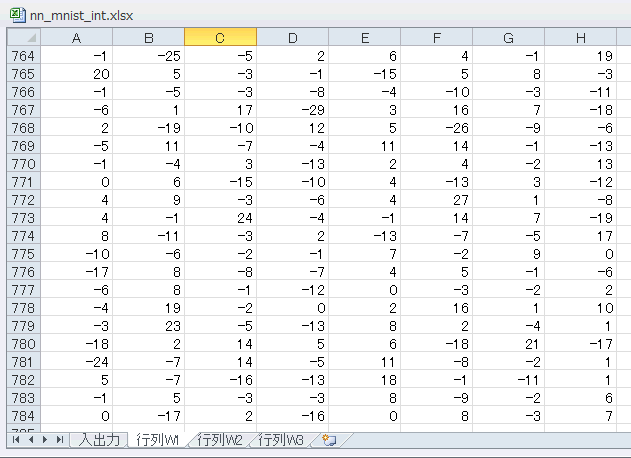 図1-16 EXCEL表の2番目のシート。重みの行列W1
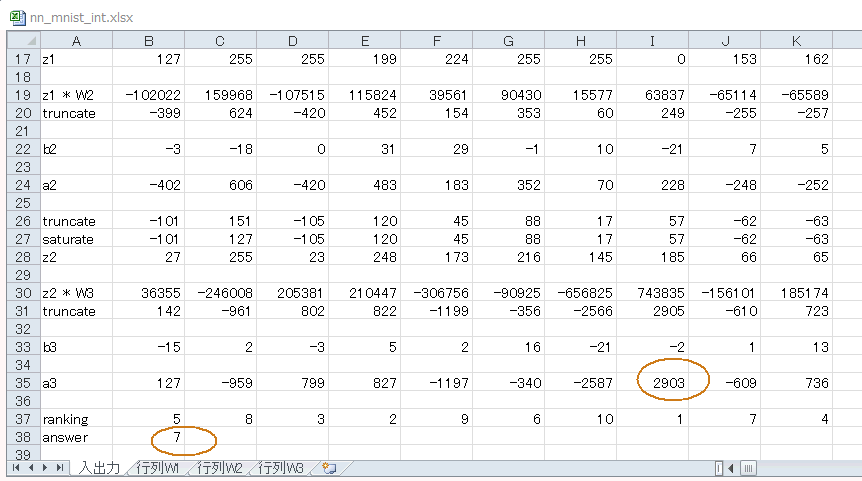 図1-17 EXCEL表の最初のシート(後半)
図1-19 Pythonで計算した推論結果も同じ値 目次へ戻る |
||||||||||||||||||||||||
1-05 PythonからEXCELに移植してみる
 図1-15 EXCEL表の最初のシート。ここで演算を行う
 図1-16 EXCEL表の2番目のシート。重みの行列W1
 図1-17 EXCEL表の最初のシート(後半)
図1-19 Pythonで計算した推論結果も同じ値 目次へ戻る |
||||||||||||||||||||||||