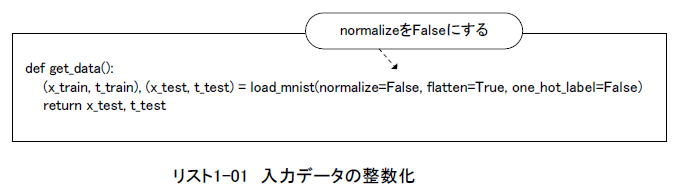
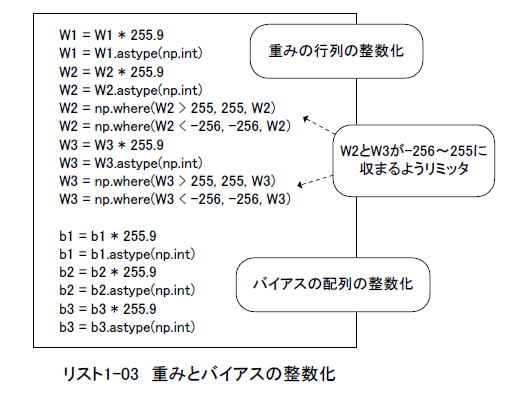
1-04　入力、重み、バイアスなどすべて整数化してみる ■Pythonのプログラムを整数化する 　パソコンで計算するぶんには小数でよいのですが、FPGAで小数の演算は行えません。したがってneuralnet_mnist.py内の変数をすべて「整数化」します。 ●入力データを整数化する 　まずは入力されるテスト画像を整数化します。リスト1-01のようにload_mnistの引数normalizeをTrueからFalseに変更すると、画像データはリスト1-02のように0〜255までの整数になります。 　リスト1-02のカッコ内は整数化する前の値です。これは(0.0〜1.0)の範囲が[0〜255]の範囲に写像されたことを意味します。 ●重みとバイアスを整数化する 　またリスト1-03のように重みの行列W1〜3、バイアスの配列b1〜3を256倍し（＊１）、型をintにするとそれらはリスト1-04のように整数になります。 （＊１）整数化後の絶対値を255以下に収めるために255.9を乗算している。またW2とW3は絶対値が1.0を超えるものがあるのでリミッタをかける 　リスト1-04のカッコ内は整数化する前の値です。(-1.0〜+1.0)の範囲が[-256〜+255]の範囲に写像されています。 ●積和演算の直後に8ビット右シフトさせる 　上述のように(-1.0〜+1.0)は整数化によって[-256〜+255]に写像されます。これは重みやバイアスの値が整数化によって256倍になることを意味します。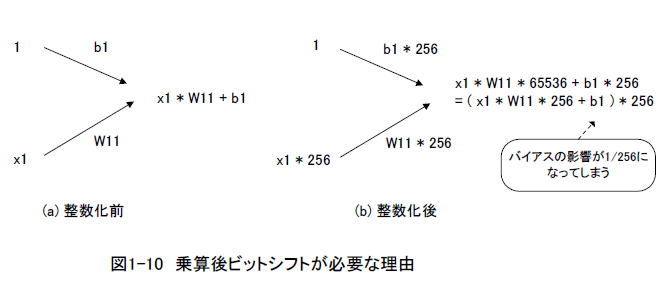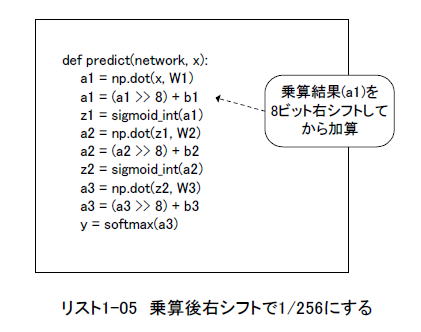 　また入力データの値も整数化によって256倍になります。それは重みと乗算されるので、その結果の値は65,536倍になってしまいます（図1-10）。バイアスの値は256倍のままなので、そのまま加算するとバイアスの影響力が1/256になってしまいます。したがってリスト1-05のように8ビット右シフトさせてからバイアスを加算します。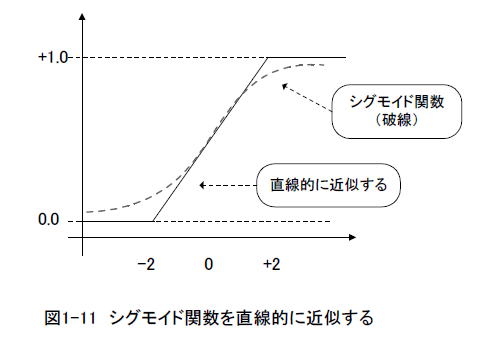 ●シグモイド関数を変更する 　シグモイド関数は数式で表すと式1-01になります。グラフで表すと図1-11の破線のようになります。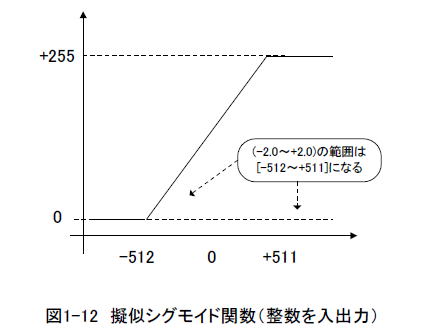 　h (x) = 1 / ( 1 + exp (-x) )　　　式1-01　シグモイド関数 　FPGA向きの特性ではないため、図1-11のように-2.0で0に飽和、+2.0で+1.0に飽和する直線的な関数で近似します。(-1.0〜+1.0)が[-256〜+255]に写像されることを鑑みると図1-12のような特性の関数になります。 　リスト1-06に変更した関数（sigmoid_int）を示します。-512で0に飽和、+511で255に飽和します。 ●整数化した値をファイルに落とす 　リスト1-07のように変更すると入力（テスト画像の最初の1枚）、重み（行列3個）、バイアス（配列3個）をファイルに書き出すことができます。後々EXCELに貼り付けるのでCSVファイルでセーブします。 ●正解率はほとんど落ちていない！ 　図1-13は整数化したプログラムを実行した結果で、正解率（Accuracy）は0.9325（93.25％）になります。整数化前は93.52％だったので１％も劣化していないことになります。 　図1-13　実行結果（整数で計算） ●PythonとEXCELを確実に一致させるために 　リスト1-08のように演算の結果や途中経過をファイルに落としておくと、後々EXCEL化やVHDL化の際、データの比較、つき合わせに役立ちます。 ●整数化すると推論に3秒程度かかる？ 　私はWindowsパソコンにAnacondaのJupyter Labをインストールしています。Pythonを整数化してテスト画像10,000枚を推論させると、3秒程度かかるようです。皆さんの環境ではどうでしょうか。 目次へ戻る