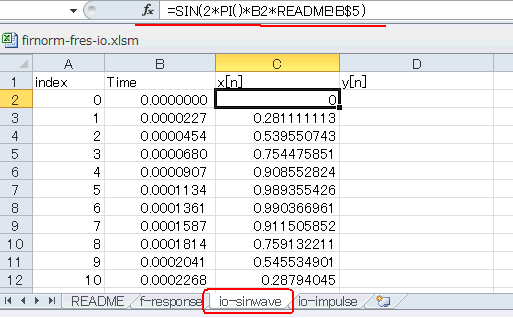
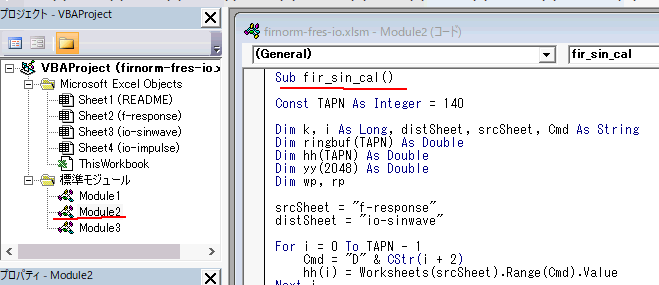
3-01　FIRフィルタのEXCELシートの説明（続き） ●サイン波の入出力を計算するシート 　隣のシートio-sinwaveを見てみましょう。A列(index)に0〜2047、B列(Time)はそれをサンプリング周波数（44100、READMEのB4セル)で割ったものです。C列(x[n])は図3‐10の式で示すようなサイン波になります（＊１）。これがFIRフィルタの入力になります。 （＊１）この例では1kHz（READMEのB5セルが1000）のサイン波になる。すなわち44100/1000サンプルで一回転（2π）する。 　　図3-10　隣のシートを見てみる ●FIRフィルタの出力を計算するVBA 　D列(y[n])はFIRフィルタの出力ですが、係数の数が140個と多いので出力もVBAで計算します。図3‐11のようにVBAウインドウからModule2を開いて実行します。 　　図3-11　リングバッファでフィルタ演算 ●出力の振幅と遅延を見る 　すると出力の計算結果がD列に反映され、更にグラフが描画されます（図3‐12）。振幅はほぼ0dB、また1.57ms程度の遅延が見られます。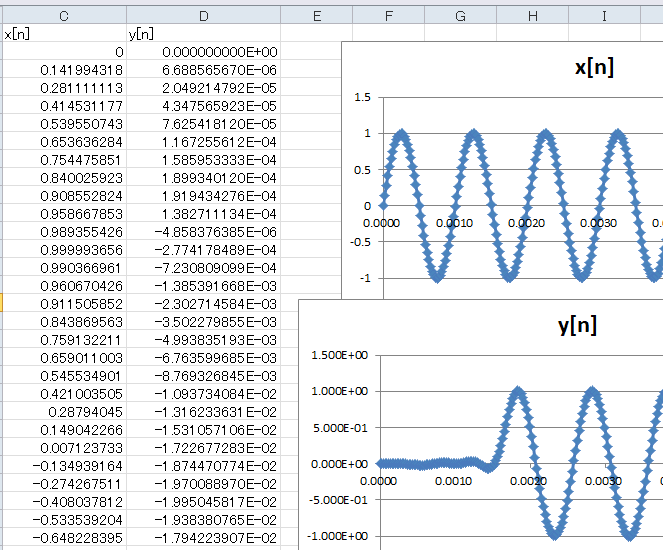 　　図3-12　右の方に入出力のグラフがある ●インパルス応答を計算するシート 　その隣のシートio-impulseではインパルス応答を計算しますが、その計算にもVBAを使用します。Module3を開いて実行しましょう（図3‐13）。 　　図3-13　VBAウインドウを開く ●インパルスの形と遅延を見る 　io-impulseシートにインパルス応答が表示されます。図3‐14のようにグラフ表示され、遅延が1.57msあることが分かります。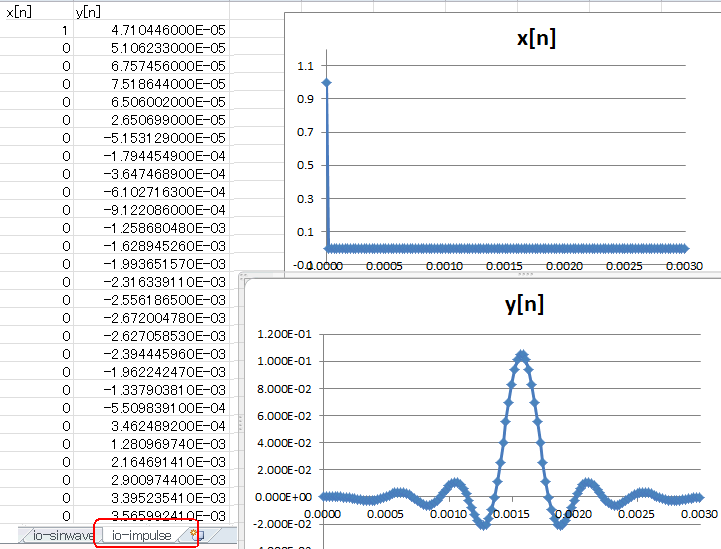 　　図3-14　出力の遅延は0.00157秒くらいある ●係数の数と遅延の関係は・・・ 　FIRフィルタの場合、インパルス応答は係数と同じになります。したがって入力に対する遅延（山の頂上の位置）は係数の数の半分くらいの位置になります。 　正確にはタップ数をNとすると、（N-1）/2 サンプルの遅延、すなわち (140-1)/2 = 69.5サンプル、それにサンプリング周期をかけて 69.5 / 44.1kHz = 1.57ms、これが遅延時間になります。図3‐12、14どちらも1.57ms程度出力が遅れているのが分かります。 　これを見ると位相特性がギザギザしていますが、実際は右下に直線的に伸びていきます（図3‐15）。これを「直線位相特性」といいます。 　　図3-15　角周波数と位相の関係 ●位相特性の傾きτは定数 　θ(ω) は位相の遅れ、τは定数なので「時間の遅れが一定」ということです。つまり周波数によらず遅延時間が同じということになります（図3‐16）。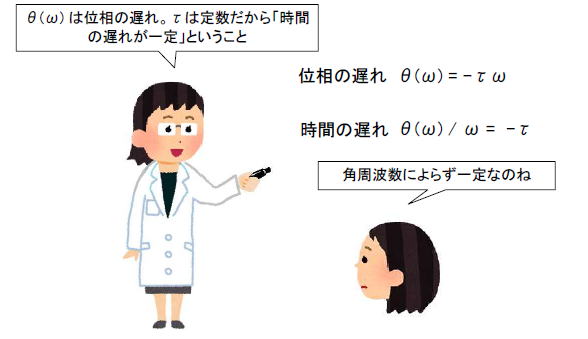 　　図3-16　位相(rad) / 角周波数(rad/s) なのでτの単位は(s) ●FIRの場合、タップ数で遅延時間が決まってくる 　つまり、直線位相特性は「群遅延時間一定特性」と言い換えることができます。図3‐12、14のようにどのような入力（周波数）でも出力が1.57ms遅延するのはそのためです。この直線位相特性はFIRフィルタの大きな特徴で、IIRフィルタでは実現できません。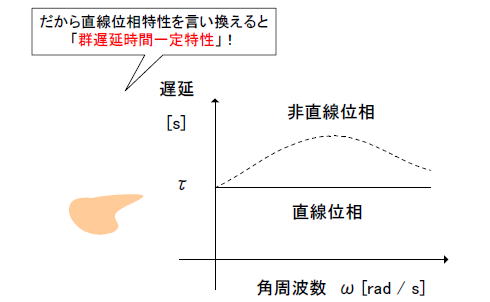 　　図3-17　遅延時間が固定なのはFIRのメリット。色々なことに応用できる！（ここ参照） 最初のページへ 目次へ戻る