arm_mult_q15関数

2つの配列の各要素を乗算する

関数のソース（CMSIS 2.0以上をダウンロード・インストールする必要あり） CMSIS_2_00\CMSIS\DSP_Lib\Source\Cortex-M4-M3\BasicMathFunctions\arm_mult_q15.c サンプルソース（DFFSKN40基板付属CD-ROMに収録） IARprojects\src\projects\arm_mult 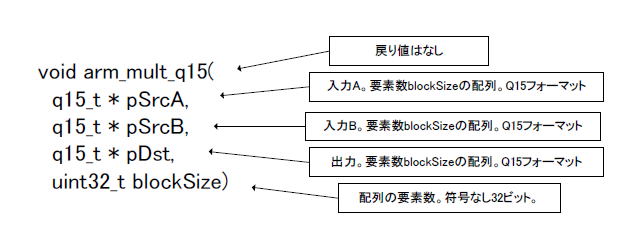引数と戻り値 説明（イメージ） 使用例（サンプルソースの一部） q15_t a[] = {10000, -12345, -30000, 100}; q15_t b[] = {20000, 22222, -13579, 200}; q15_t c[] = {0, 0, 0, 0}; 　：　中略 arm_mult_q15( a, b, c, 4 ); この関数を実行すると配列cの中に結果が入っている。 実験 上記のサンプルソースをDFFSKN40基板（デジタルフィルター社）にて実験した。Cortex-M4マイコンはPK40X256VMD100（Kinetis, フリースケール社）搭載。演算結果をLCDに16進数で表示している。 下の写真はn = 0のとき。 a[0] = 10,000, b[0] = 20,000なので、 10進数で：　10,000 * 20,000 = 200,000,000 16進数で：　0x 0BEB C200　（32ビットになる） 2進数で：　0000 1011 1110 1011 1100 0010 0000 0000 15ビット右シフトして：　0001 0111 1101 0111 16進数で：　0x 17D7 10進数で：　6103 = c[0] 下の写真はn = 1のとき。 a[1] = -12,345, b[1] = 22,222なので、 10進数で：　-12,345 * 22,222 = -274,330,590 16進数で：　0x EFA6 0C22 2進数で：　1110 1111 1010 0110 0000 1100 0010 0010 15ビット右シフトして：　1101 1111 0100 1100 16進数で：　0x DF4C 10進数で：　-8372 （最上位ビットが1なので負の数）= c[1] 下の写真はn = 2のとき。 a[2] = -30,000, b[2] = -13,579なので、 10進数で：　-30,000 * -13,579 = 407,370,000 16進数で：　0x 1847 F910 2進数で：　0001 1000 0100 0111 1111 1001 0001 0000 15ビット右シフトして：　0011 0000 1000 1111 16進数で：　0x 308F 10進数で：　12,431 = c[2] 下の写真はn = 3のとき。 a[3] = 100, b[3] = 200なので、 10進数で：　100 * 200 = 20,000 16進数で：　0x 0000 4E20 2進数で：　0000 0000 0000 0000 0100 1110 0010 0000 15ビット右シフトして：　0000 0000 0000 0000 16進数で：　0x 0000 10進数で：　0 = c[3] まめ知識 極値同士の乗算はオーバフローになることがある。 �@0x7FFF * 0x7FFF = 0x7FFE �A0x7FFF * 0x8000 = 0x8001 �B0x8000 * 0x8001 = 0x7FFF �C0x8000 * 0x8000 = 0x7FFF �@、�A、�Bは上述の算法に沿った結果と同じであるが�Cは、 10進数で：　-32,768 * -32,768 = 1,073,741,824 16進数で：　0x 4000 0000 2進数で：　0100 0000 0000 0000 0000 0000 0000 0000 15ビット右シフトして：　1000 0000 0000 0000 ←正の数なのにMSBが1になっている。 この場合はオーバフローであり、正の最大値0111 1111 1111 1111 に置き換えられる。 16進数で：　0x 7FFF 10進数で：　32,767　これが乗算結果となる。

戻る

Top Page