コラム11　フーリエ変換を理解する ●信号解析の基本はフーリエ変換 　デジタル信号処理には大雑把に言って「信号を解析する」手法と「信号を処理する」手法が存在します。前者の代表格は「デジタルフィルタ」であり、後者の代表格は「FFT」（Fast Fourier Transform、高速フーリエ変換）です。 　本章ではまず「フーリエ変換」から説明します。フーリエ変換をデジタル化したものがDFT(Discrete Fourier Transform、離散フーリエ変換)、DFTを高速化したものがFFTになります。それらについては追って説明します ■フーリエ変換の式が意味するものは何か？ ●フーリエ変換の定義 　前出マンガ11中の式1-1はフーリエ変換の定義です。この式におけるe^-j 2πftは回転因子(Twiddle Factor)と呼ばれ、その物理的な意味はオイラーの公式（式1-2）を考慮に入れると、絶対値が１で、周波数fで回転する複素ベクトルになります（図1-20）。 　そして時間軸の信号x(t)に回転因子を乗算し、積分により累積するのがフーリエ変換です。 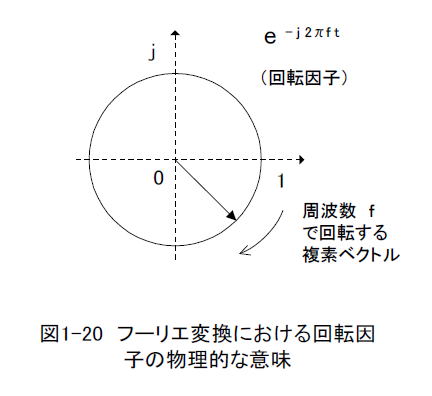●虚数単位は"i"ではなく"j"と表記する 　数学の世界では虚数単位は"i"と表記しますが、電気工学の世界では「電流」をそう表現することが多く、混同を避けるために虚数単位を"j"と表記します。 ●直流から高い周波数まで、任意の周波数を調べることができる 　マンガ11では「スマホアプリ」を使ってフーリエ変換のイメージを伝えました。その際の「回転因子」は10Hz, 20Hz, 30Hz, ... 90Hzと9種類でしたが、実際のフーリエ変換では0Hzから無限Hzまで任意の実数値を取り得るので、スペクトルX(f)は連続的になります。 ●フーリエ変換を施すとスペクトルが得られる 　マンガ11で説明したように、フーリエ変換とは「回転因子の周波数と入力信号のシンクロ具合」を観察する作業のことで、その結果が周波数分布（スペクトル）になります。 ■スペクトルが分かると何がおいしいのかを実感しよう！ 　スマホアプリの「FFTとフィルタを体感しよう！」をタップするとFFT(高速フーリエ変換、コラム13で説明)を体感できます。 ●周波数軸にすると音の正体が分かる 　スマホに向かって「ドレミファソラシド」すれば人の声の基音や倍音を確認できます。またクラッシック音楽に重畳したノイズの周波数なども知ることができます。ぜひ試してみてください。 ●信号の分析や処理にはフーリエ変換が必須！ 　このようにスペクトルにより必要な成分と不要な成分が分かり、それによりフィルタの特性を決定できます。そしてスペクトルを得るために必要となるのが「フーリエ変換」なのです。 目次へ戻る