コラム12　DFTを理解する ●計算機でフーリエ変換するために考えられたDFT 　前節でフーリエ変換のイメージを掴んで頂けたと思います。それでは早速実践してみよう・・・とパソコンに向かってみると一つ疑問が湧くでしょう。 　積分のプログラムってどう書くんだっけ・・・？？ ●フーリエ変換は実践向きじゃない！？ 　計算機において連続時間信号を積分するのは難しいです。さらにフーリエ変換の定義（前出のマンガ12内の式1-1）を見ると入力信号はx(t)となっていますが、入力信号が何らかの数式で表現できるのは極めてまれです。したがって、実際のフーリエ変換の計算には「離散時間信号」を適用します。 ■離散時間信号をフーリエ変換するDFT 　式1-3はDFT(Discrete Fourier Transform、デジタルフーリエ変換)の定義です。 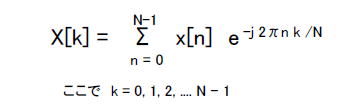式1-3　DFTの定義 　フーリエ変換（式1-1）と比較してのメリットは次のようになります。 �@演算は乗算と加算のみ（積分が要らない） �A入力は離散時間信号（数字の羅列でよい） ●回転因子も離散的な角度をとる 　e^-j 2πnk/Nは回転因子（Twiddle Factor)とよばれ、周波数k/Nで離散的な角度をとりながら回転します（図1-40）。 ●入力信号の数もN個、DFTの結果もN個になる 　回転因子にサンプル数N個の離散時間信号x[n]を乗算し、それらを累積加算します。DFTの結果はサンプル数N個の離散的なスペクトルX[k]になります。 ●逆DFTも定義されている 　また、DFTに対して逆DFT(IDFT, Inverse DFT)の定義を式1-4に示します。DFTとの違いは回転因子のまわる方向が逆になること、乗算累積結果をNで除算することの二つです。 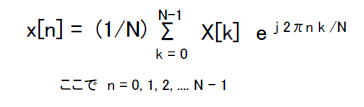式1-4　逆DFTの定義 ●回転因子の各周波数 　また、DFTにおける回転因子の角周波数は、その周波数がk/Nであることから次のようになります。 　式1-5 ●DFTの結果は左右対称になるのでスペクトルの左側だけを見る 　マンガ中の図1-34のx[n]は「0.1Hzのサイン波を1.0Hzでサンプリングしたもの」であり、0.9Hzのサイン波は含まれていません。したがって、DFTの結果として有効なのはナイキスト周波数（サンプリング周波数の半分）までになります。0.5Hzから0.9Hzは周波数成分としては無視してください。 ●正規化周波数でDFTを行い、結果にサンプリング周波数をかける 　このアプリでは周波数は正規化（サンプリング周波数を1.0Hzとして考える）されていますが、実際のシステムはそれぞれ固有のサンプリング周波数を持っています。 　例えば図1-34のx[n]のサンプリングが「100Hz」だったらどうなるでしょうか？その場合はX[k]の周波数軸のスケールを単純に100倍します。X[k]は左から10, 20, 30, 40Hzとなるので、x[n]には「10Hz」のサイン波だけが存在することになります。 ●FREQボタンでいろいろな入力信号をDFTしてそのイメージを掴もう 　DFTの定義(式1-3）は一見複雑に見えますが、要は「(k/N)という周波数で回転因子を回して入力信号と乗算して累積する」ということです。その作業によって「回転因子と入力信号のシンクロ具合」が得られ、それがスペクトルになります。スマホアプリをじっとご覧になればそれを実感できることでしょう。 ●「フーリエ変換」を実践向きにする「DFT」 　DFTの演算は乗算と加算で済み、積分は必要ありません。また入力信号はx[n]といった数列でよく、数式でモデリングする必要もありません。 　このようにDFTによって、フーリエ変換がパソコンで簡単に計算できるようになったのです！ 目次へ戻る