コラム17　なぜ窓関数をかけるのか 　「N点FFT」という作業は「N個のデータを繋ぎ合わせて周期化した信号のフーリエ級数」（＊１）と等価です。 （＊１）周期的な信号に適用されるフーリエ変換。周期をTとすると、(1/T), (2/T), (3/T), ... (n/T)といった整数倍の周波数のみが成分を持つ。 ●窓関数がないと「繋ぎ目」ができる 　図1-100は矩形窓（窓関数なしと一緒）の場合です。周期化した結果、繋ぎ目の部分で高周波や直流成分が発生します。この状態ではスペクトルのフロアが上がってしまい、微小成分は観測しにくくなります。 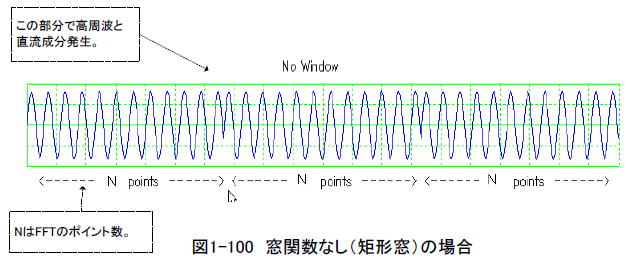●窓関数で繋ぎ目をなくす 　図1-101のようにHanning窓を施すと繋ぎ目の高周波と直流分が減少します。こうすればスペクトルのフロアはぐっと下がり、微小成分でも観測できるようになります。 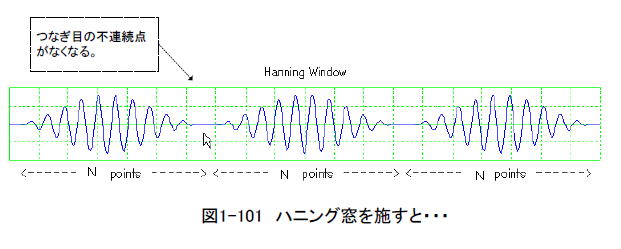●FFTでよく使われる窓関数5種類 　図1-102に窓関数を5種類示します。同図はN点FFT用の窓関数であり、N個の入力データに掛け合わせた後にFFT演算します。 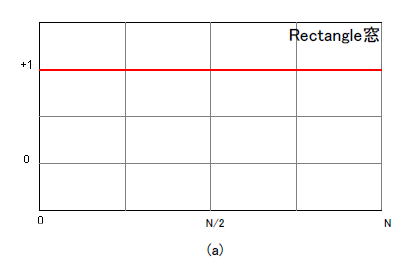　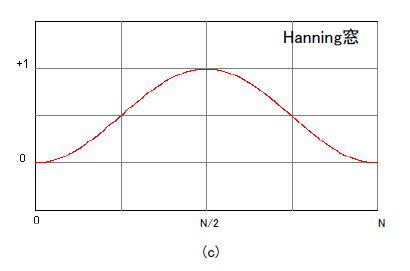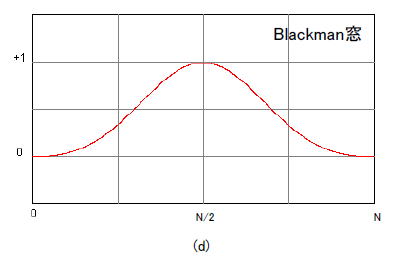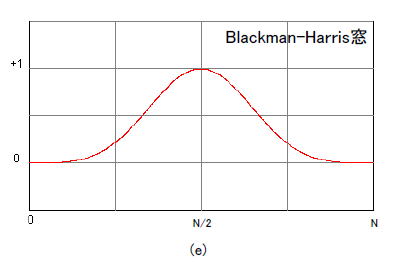図1-102　5種類の窓関数 　マンガ内の表1-3に示すように窓関数にはそれぞれ長所と短所があります。目的や用途によってうまく使い分けましょう。 目次へ戻る