コラム29　畳み込みのイメージをつかもう ●FIRフィルタの差分方程式は畳み込みの一種 　漫画26で紹介したスマホアプリ、「群遅延時間とは」では入力データx[n]と係数h[n]の畳み込みを行いました。数式で表すと次のようになります。 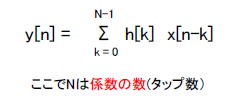　　式2-30　FIRフィルタの差分方程式（畳み込み） 　上式では次のように畳み込みを行います。 �@入力データx[n]をkサンプル遅延させて(x[n-k])とする。 �Aその遅延データに対応する係数h[k]を乗算する。 �Bその乗算データを累積する。 　畳み込みは「＊」という記号で表し、次のような「交換律」が成立します。 　　式2-31　畳み込み演算の交換律 ●FIRフィルタの差分方程式のもう一つの姿 　ここで入力データや係数の定義域外の値を0と再定義した後、畳み込みの交換律を適用すると式2-30は式2-32と等価になります。 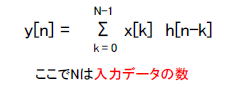　　式2-32　FIRの差分方程式の別の表現 　上式では次のように畳み込みを行います。 �@係数h[n]をkサンプル遅延させて(h[n-k])とする。 �Aその遅延係数に対応する入力データx[k]を乗算する。 �Bその乗算データを累積する。 ●スマホアプリで畳み込みのイメージをつかむ！ 　それでは式2-32の物理的なイメージをスマホアプリで説明します。図2-111のように「畳み込みのイメージ」をタップしましょう。 　　図2-111　スマホアプリの第2部から選択 �@係数ボタンで適当に（例えば５タップ移動平均）選択し、Click me again and againを繰り返しタップしてください。 �Aなぜ畳み込みによってフィルタリングが達成されるのか、そのイメージを捉えましょう。 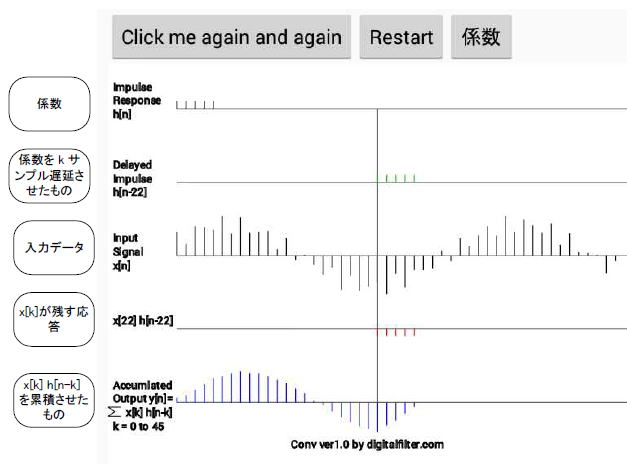　　図2-112　畳み込みのイメージが描かれる ●「入力のある一点が残す応答を累積する」ということ 　この演算の意味は次のようになります。 �@入力信号のある一点(x[k])が残す応答が(x[k] h[n-k])になる。 �Aそれをすべての点x[k], k = 0, 1, 2, …, N-1（Nは入力データの数）において計算する。 �Bそれらを累積する。 　一連の作業を数式で表すと式2-32になりますが、数式そのものよりも、その物理的な意味を理解しましょう。 目次へ戻る