| コラム22 畳み込みを単純な乗算に変えるラプラス変換とZ変換 ■アナログフィルタの伝達関数はラプラス変換された式で表現される 式2-4はラプラス変換の定義式です。 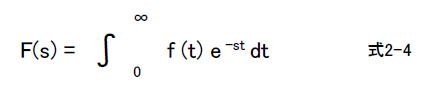 ●入力とインパルス応答を畳み込み演算すれば出力が得られる システムの特性はインパルス応答で決定され、図2-42ではそれをh(t)としています。 このシステムにx(t)が入力された場合の出力y(t)は、同図内式2-5のように求めます。同式は「畳み込み」とよばれますが、積分が必要であり、計算機等で行うには困難を伴います。  図2-42 ラプラス変換した世界で出力を求める ●畳み込みはやりたくない・・・ そこで考えられたのがラプラス変換です。 ①x(t), h(t)をラプラス変換し、X(s), H(s)とします。 ②ラプラス変換したもの同士を乗算しY(s) = X(s) H(s)とします。 ③それを逆ラプラス変換すればシステムの出力y(t)が求まります(畳み込み演算が要らなくなる)。 ●ラプラス変換した方がシステムが分かりやすくなる また図2-43のようにシステムAとシステムBを縦続接続する場合、システム全体の伝達関数は単純な乗算A(s) B(s)となります。 ラプラス変換により、複雑な畳み込み演算が単純な乗算になります。そのような理由で連続時間信号(アナログ)システムにおいてラプラス変換がよく使われます。 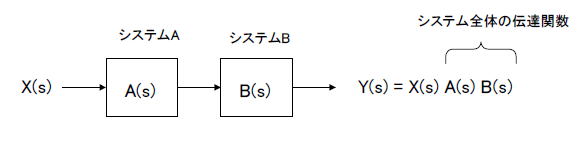 図2-43 2つのシステムの伝達関数を単純に乗算すればよい ■デジタルフィルタの伝達関数はZ変換された式で表現される 式2-6はZ変換の定義式です。 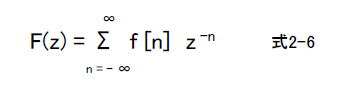 ●入力とインパルス応答を畳み込み演算すれば出力が得られる デジタルフィルタの場合も同様に、システムの特性はインパルス応答で決まります。それは離散信号なのでh[n]と表現します(図2-44)。 このシステムに入力x[n]が入力された場合の出力y[n]は、同図内式2-7のように求まります。この式は「畳み込み」のデジタル版です。 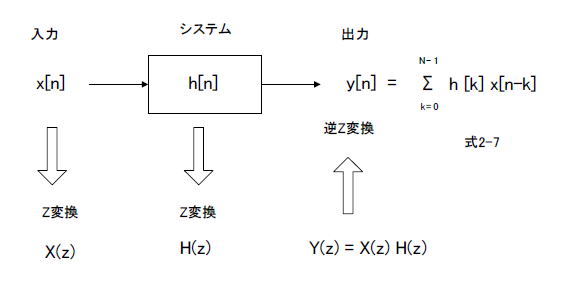 図2-44 Z変換した世界で出力を求める ●Z変換すると、単純な乗算で出力が求まる Z変換を行うと畳み込み演算しなくても出力が求まります。 ①離散信号システムではx[n], h[n]をZ変換し、X(z), H(z)とします。 ②Z変換したもの同士を乗算しY(z) = X(z) H(z)とします。 ③それを逆Z変換すればシステムの出力y[n]が求まります。 ●Z変換した方がシステムが分かりやすくなる また図2-45のようにシステムAとシステムBを縦続接続する場合、システム全体の伝達関数は単純な乗算A(z) B(z)となります。 Z変換により、複雑な畳み込み演算が単純な乗算になります。そのような理由で離散時間信号(デジタル)システムにおいてZ変換がよく使われます。 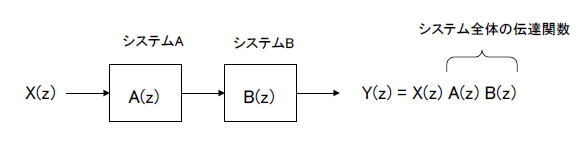 図2-45 2つのシステムの伝達関数を単純に乗算すればよい 目次へ戻る |