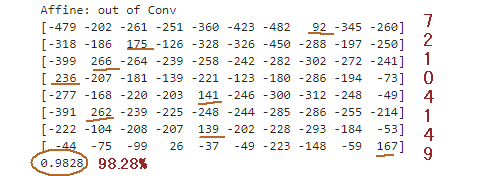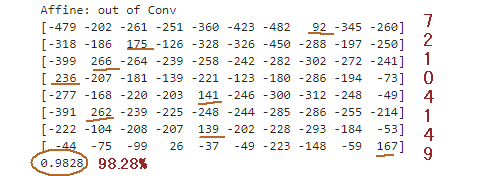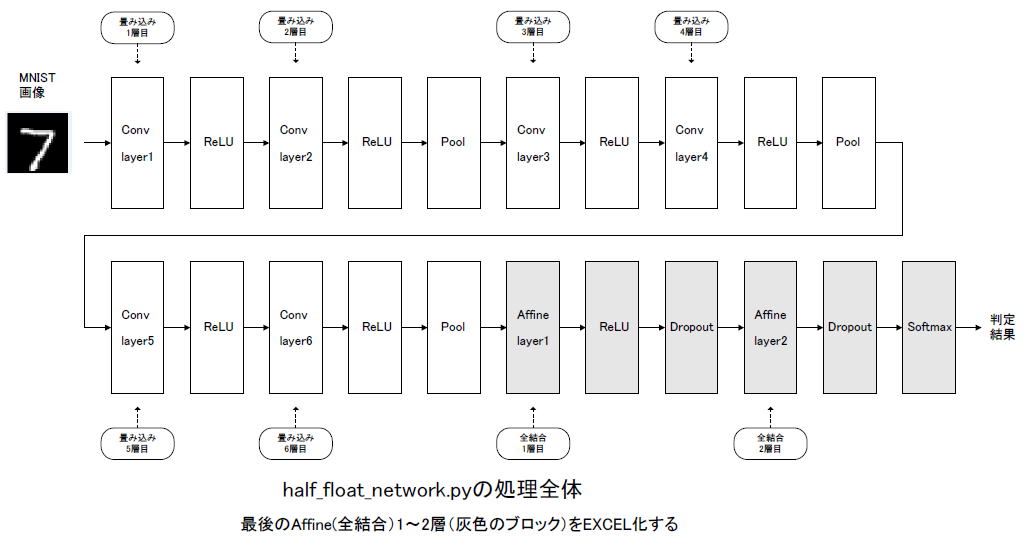
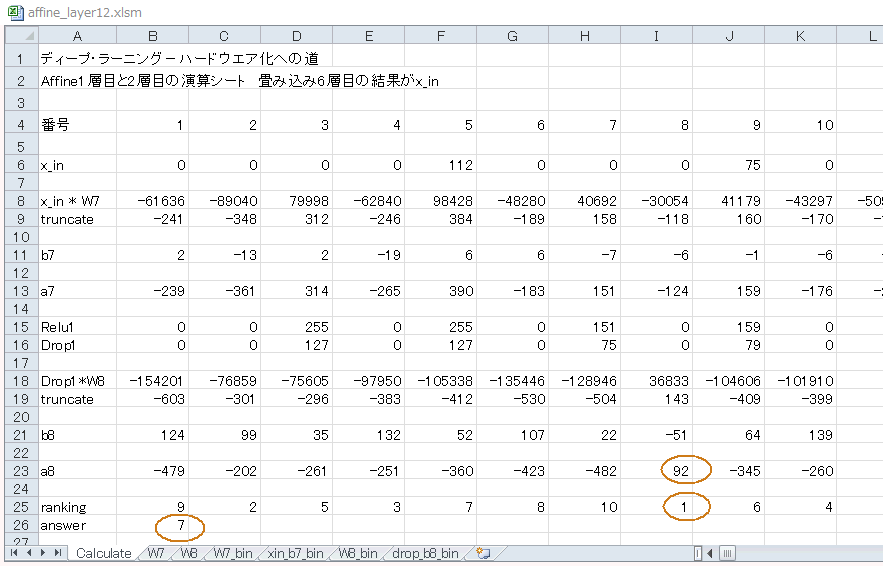
9-01　Affine（全結合）層をEXCEL化する ●畳み込み6層の後に全結合が2層ある 　今回ハードウエア化を試みる畳み込みニューラルネットワークの全体像を図9-01に示します。この書籍の8章、half_float_network.pyというPythonプログラムの流れをブロック図にしたものです。 　図9-01　処理の全体像。畳み込みが6層、その後全結合が2層ある ●Affine１層目と２層目のEXCEL化 　まずはAffine（全結合）層をPythonからEXCELに移植します（ここにそのファイル）。図9-02にEXCEL表の最初のシートを示します。このシートで計算を行います。 　第1部で全結合ニューラルネットワークをEXCEL化しましたが、それとの主な違いは、シグモイド関数の代わりにReLU関数を用いるところです。 　図9-02　EXCEL表の最初のシート。ここで演算を行う ●MNISTの最初の数字は”７” 　上図のDrop1行（＊１）がAffine1層目の結果、a8行がAffine2層目の結果です。a8が最大になるのが7番目なのでanswerは”７”（＊２）、これが「畳み込みニューラルネットワーク」の最終結果になります。図9-03はMNISTのテスト画像の最初の一枚で、数字の７であり、正解であることが分かります。 （＊１）Dropoutの結果。この例おいてはReLU結果を0.5倍して出力するだけ。 （＊２）SoftMaxの結果でこれが推論値。最大値が何番目かを出力する。その前のDropoutは省略してある 　図9-03　MNISTの最初の画像 ●Phtyonと同じ結果になることを確認 　図9-04はPythonでの推論結果です。最初の行がMNIST1枚目（数字の７）で、図9-02のa8行とピタリ一致していることが分かります。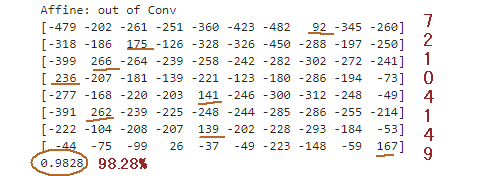 　図9-04　Pythonでの推論結果（MNIST最初の8枚） ●Affine1層目の重み行列は1024×50 　畳み込み6層目の結果は64チャネル、それぞれ4×4画素でした。それらを横一行に並べたものが図9-02のx_in行で、4x4x64 = 1024列にわたります。 　したがってそれらに乗算する重み係数は図9-05のように1024行となります。同図では列が50列なので行列乗算の結果は1行×50列になります。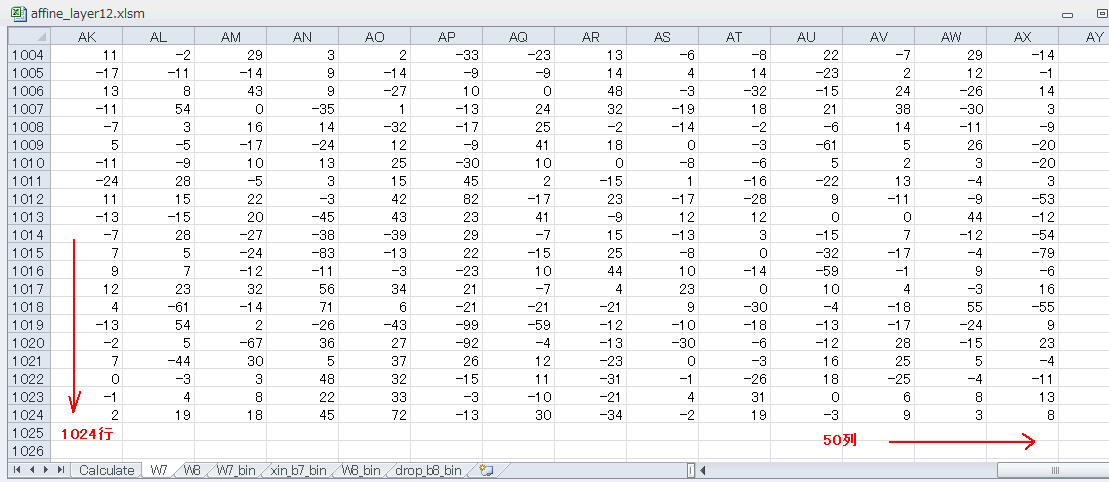 　図9-05　シートW1がAffine1層目の重み行列 ●Affine2層目の重み行列は50×10 　Affine1層目の結果は1行×50列なので、それらに乗算する重み係数は図9-06のように50行となります。同図では列が10列なので行列乗算の結果は1行×10列になります。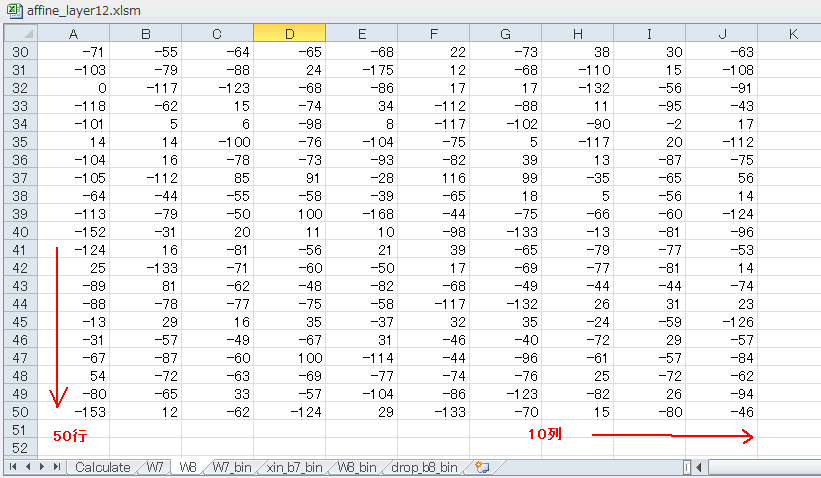 　図9-06　シートW2がAffine2層目の重み行列 目次へ戻る