7-01 2層目は乗算器が256個も必要になる?
●1層目は入力チャネル数(画像枚数)が1だった
前章で畳み込み1層目をVHDL化しましたが、その際、乗算器16個を並列動作させました。図7-01に示すようにフィルタが16種類あり、それぞれに対して1個の乗算器を割り当てます。各フィルタは9個の係数を持つため、入力画像1枚を処理するのに9×28×28=7,056サイクルかかります。 |
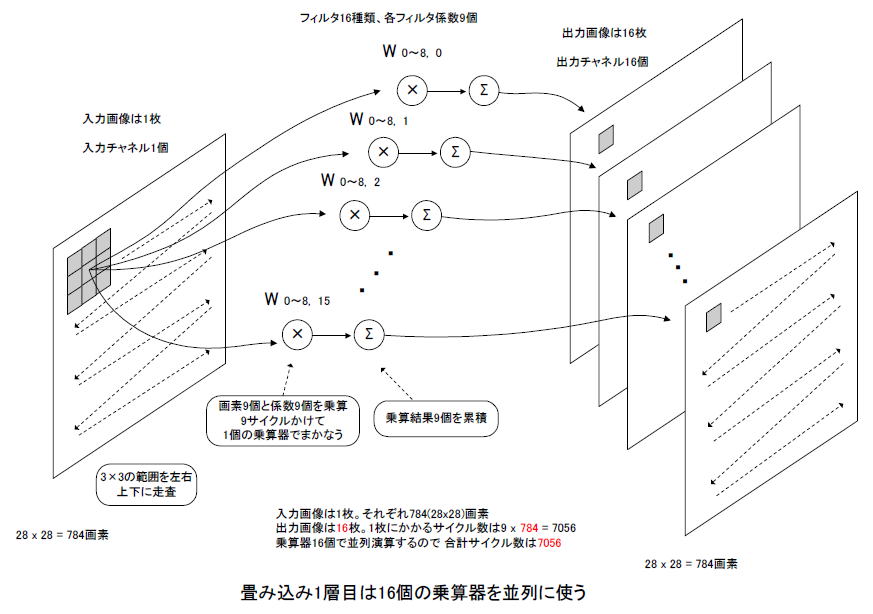
図7-01 畳み込み1層目の演算のイメージ
●2層目は入力チャネル数(画像枚数)が16もある
それでは畳み込み2層目はどうなるでしょうか?
1層目は入力画像が1チャネルでしたが、2層目は図7-02のように16チャネルあります。したがって2層目を7,056サイクルで処理させるには同図のように乗算器の個数が16倍、256個必要になります。 |
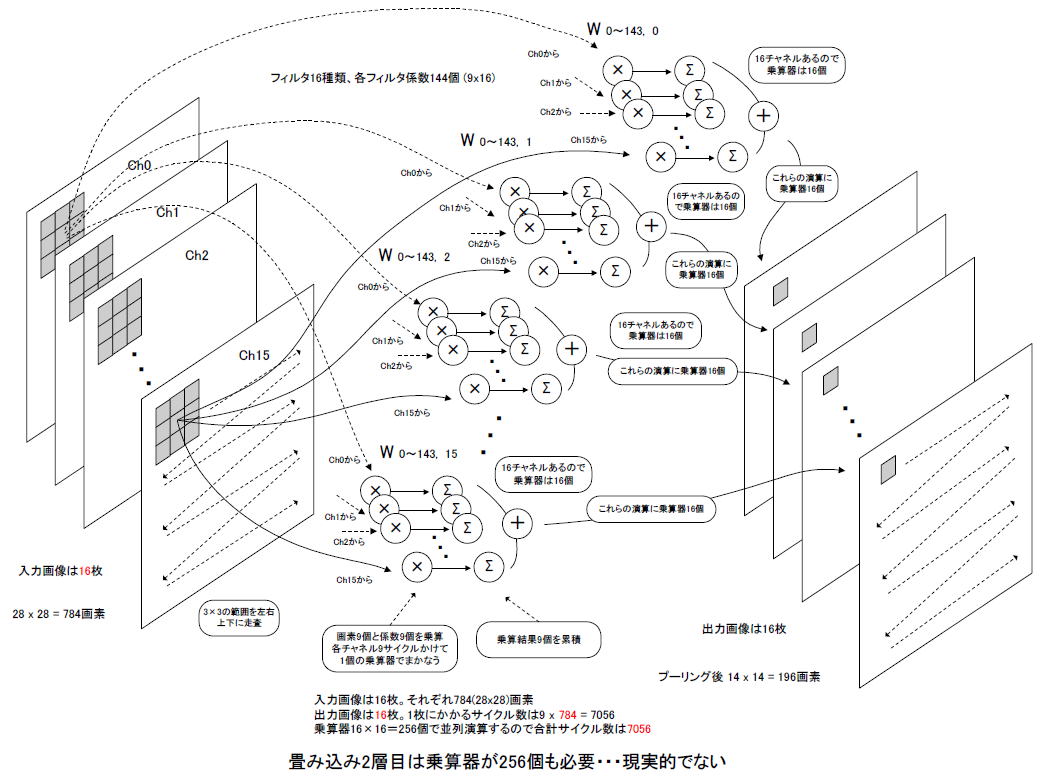
図7-02 畳み込み2層目の演算のイメージ
●安価なFPGAは乗算器を256個も持たない?
例えばこのボード上のFPGAは乗算器が80個しかありません。したがって図7-02のような方式は使えないことが分かります。
かといって乗算器の数を256/16 = 16個と減らせば、1層目と比べてサイクル数が16倍となり、後々のパイプライン化の足かせになってしまいます(足かせの意味はここ)。
したがって2層目は違ったアプローチが必要になります。ここはちょっと発想を変えて「フィルタ係数」に注目してみましょう。
表7-01は係数を整数化する際の対応です。「符号付き9ビットで整数化」とは、-1.0〜+1.0の範囲が-256〜+255の範囲に写像されることを意味します。 |
|
| 整数化前 |
整数後 |
| +1.0 |
+255 |
| +0.5 |
+128 |
| +0.25 |
+64 |
| +0.125 |
+32 |
| +0.0625 |
+16 |
| -0.0625 |
-16 |
| -0.125 |
-32 |
| -0.25 |
-64 |
| -0.5 |
-128 |
| -1.0 |
-256 |
表7-01 係数を符号付き9ビットで整数化した際の対応表 |
●乗算器を使わない乗算?
ハードウエアにおいて数値は2進数で扱われます。したがって表7-01に示すような係数値(2の累乗)の場合、乗算は「ビットシフト」でまかなえます。
例えば+64という係数をかけるなら6ビット左シフト、+16をかけるなら4ビット左シフトで済みます。-64や-16をかけるならなら符号を反転した後、同様にシフトさせます。このようにすれば乗算器を削減できそうです。 |
目次へ戻る |



