7-03　乗算器の代わりになる回路の設計 ●係数が2の累乗ならビットシフトで間に合いそう 　ここに示すように、畳み込み2層目は256個もの乗算器が必要になります。しかし比較的安価なFPGAはそんなにたくさんの乗算器を持っていません。 　前節では係数を4種類(+64, +16, -16, -64）のみに制限しても正解率がそれほど落ちないことを確認しました。本節ではその際の回路がどうなるかを考えます。 ●乗算器の代わりになる回路 　ハードウエアにおいて数値は2進数で扱われます。したがって係数が2の累乗に限られる場合、乗算は「ビットシフト」でまかなえます。 　さらに係数が4種類(+64, +16, -16, -64）に限られる場合、その回路は図7-16のようになります。画素データPIXDATAの全ビットが反転され、さらに1が加算されます。これは「-1倍」を意味します。 　係数COEFFの最上位ビットは符号ビットで、０ならPIXDATA、１ならPIXDATA×(-1)がセレクタで選択されます。 　セレクタの出力は4ビット、6ビット左シフトされ、16倍、64倍の値が生成されます。 　最後にCOEFFの値が±16か±64かによってセレクタを切り替えます。これにより+64の場合は64倍、+16の場合は16倍、-16の場合は-16倍、-64の場合は-64倍の値が出力されMULOUTとなります。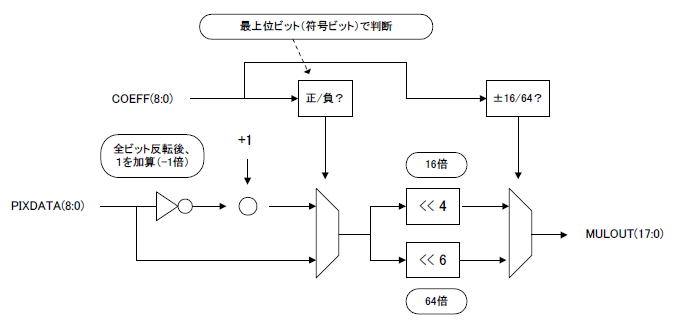 　　図7-16　乗算器の中身の回路 ●１を足すだけならハーフアダーで済む 　図7-16には加算器(+1)がありますが、これは「ハーフアダー」というシンプルな回路でまかなえます（図７-１７）。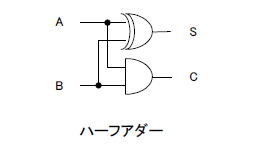 図7-17　A, Bが入力、Sが加算出力、Cはキャリー出力 ●9ビットなのでハーフアダーを9個縦続接続 　ハーフアダーをビット数ぶん（９個）、図７-18のように繋げば「＋１」の回路の完成です。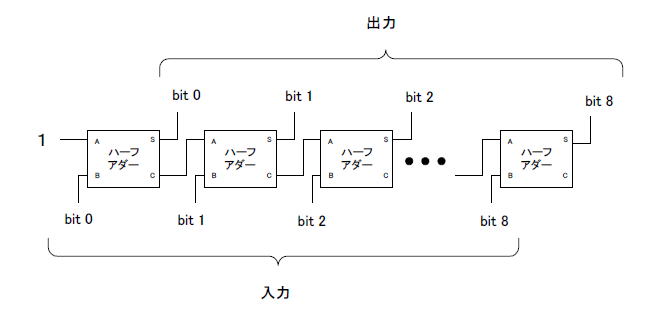 　　図7-18　ハーフアダーはそれぞれAND, EXORからなる ●シンプルな回路なので256個あっても大丈夫 　乗算器を256個も用意するのは現実的でないということで、「乗算器の代わりになる回路」を設計しました。このようにNOT, AND, EXOR、シフタ、セレクタなど単純なロジックで構成されるため、256個あってもFPGAのリソースをそれほど圧迫しないでしょう。 ●回路図をVHDL化する 　図7-16をVHDL化したもの（モジュール名SHIFMUL）がリスト7-03です。MULOUTは9ビット同士の乗算結果なので18ビットになります。ビットシフトした際、下位ビットは０で埋めます。なおVHDLにおいて”＆”はビットの結合を意味します。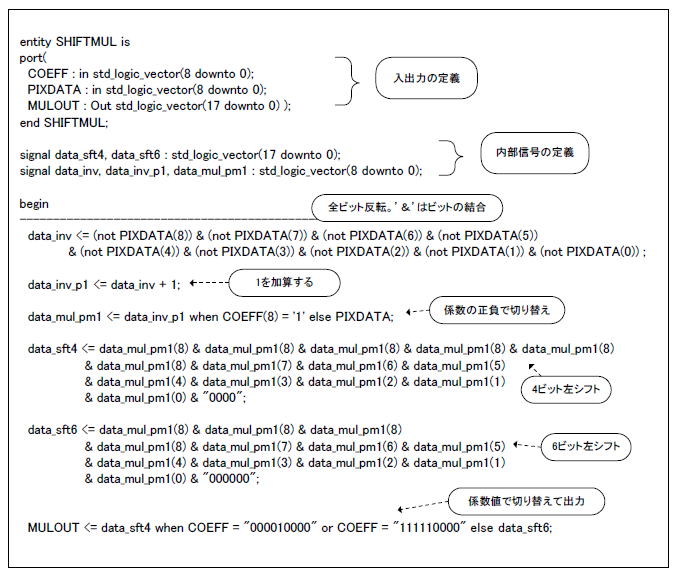 　　リスト7-03　SHIFTMUL.vhd 目次へ戻る