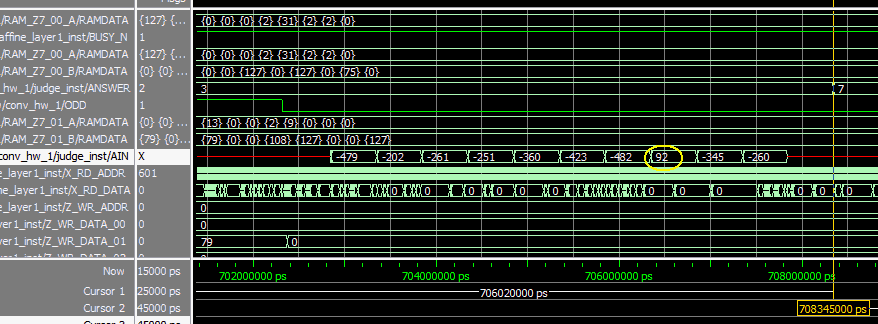
 �@�}10-14�@Python�̌��ʁi�}10-17��1�s�ځj�Ɣ�r���Ă݂悤
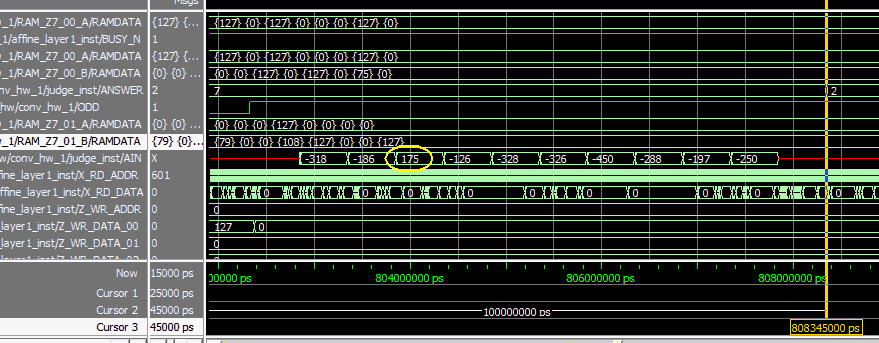 �@�@�}10-15�@Python�̌��ʁi�}10-17��2�s�ځj�Ɣ�r���Ă݂悤
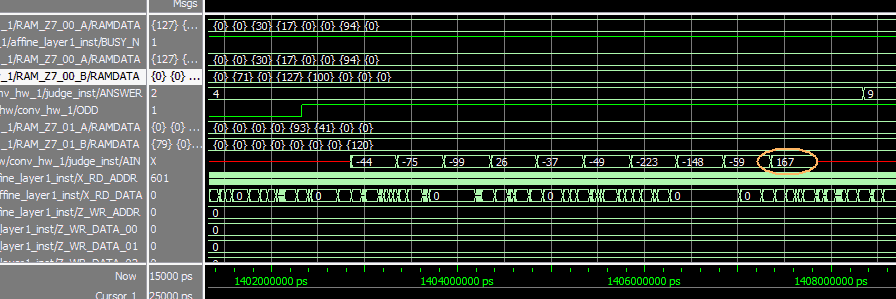 �@�@�}10-16 Python�̌��ʁi�}10-17��8�s�ځj�Ɣ�r���Ă݂悤
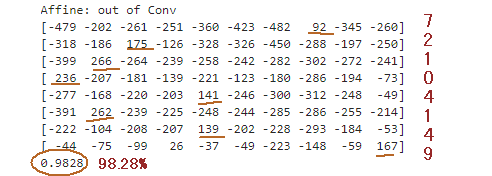 �@�@�}10-17�@Anaconda jupyter lab��Python�𑖂点������
�@�@�\10-02�@�摜�̖����������ƃ��C�e���V�̉e�������Ȃ��Ȃ�
�@�@�@�@�\10-03�@�e�w�ɂ����鎞�ԁiMNIST�摜1��������A1�T�C�N�� = 10ns)
�ŏ��̃y�[�W�� �ڎ��֖߂� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||