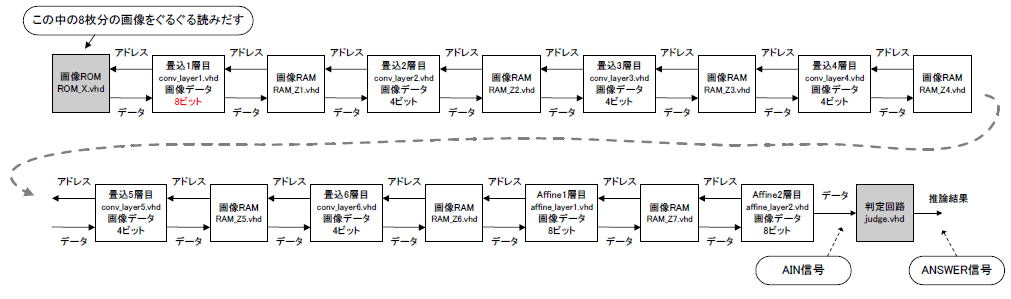
12-01　ROM内の画像8枚がFPGAで正しく推論されていることを確認 　前章では「畳み込みニューラルネットワーク」がFPGAに収まるよう回路規模を削減しました。そのブロック図を図12-01に示します。画像ROMの中にはMNISTの最初の8枚の画像データが入っており、それらを繰り返し読み出して畳み込み1層目の入力とします。 　最後の判定回路の入力AINにはAffin2層目の結果が入力されます。判定回路の出力ANSWERからは推論結果（0から9までの値、4ビット）となり、FPGAの外部に出力されます。 　　図12-01　画像ROMからの8枚が繰り返し推論される ●FPGAをオシロであたって推論結果を見る 　FPGAはIntel社のCycloneVなので、Quartus Primeというツールでプロジェクトを作成し、コンパイルの後、書き込みます（その手順はここ）。写真12-01のようにコネクタGPIO 1の右上の4ピンからANSWER信号が出てきます。 　　写真12-01　Terasic社のDE1-SoCをこのようにセットアップして書き込む ●シミュレーション通りに動いている！ 　ANSWER信号をオシロで確認したものが写真12-02です（プローブが2本しかないので合成写真）。推論結果は７，２，１，０，４，１，４，９と続きます。またその周期はシミュレーション通り100usになっています（＊１）。 （＊１）クロック周期10ns×10kサイクルでピタリ100us、常にこの値になる。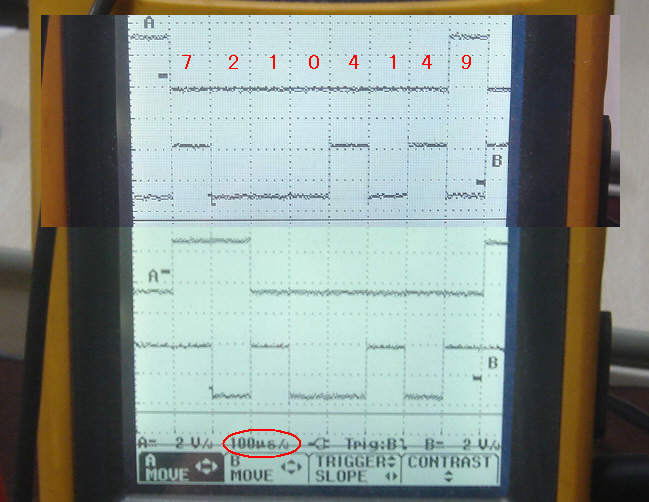このように「推論にかかる時間が正確に見積もれる」ことがFPGAの強みである（パソコンやラズベリーパイではこうはならない） 　　写真12-02　正しい推論結果が100us周期で出てくる ●Pythonと同じことがFPGA内部で起こっている 　図12-02は同じ推論をPythonで行った結果です。畳み込みニューラルネットワークでは複雑な演算を行いますが、所詮は整数の掛け算と足し算です。言語がPythonだろうがVHDLだろうが同じ結果になります。そしてVHDLをFPGAに正しくインプリすれば当然結果は一致し、正解率も同じ（98.53%)になるはずです。 　　図12-02　Pythonの結果と確認（Anaconda Jupyter Labで動作） ●無償で使えるロジックアナライザSignalTapでFPGA内部を見る 　Quartus PrimeにはSignalTapというロジックアナライザ（＊２）機能があります。図12-03はAffine2層目の出力AINを観測したものです。７＋１番目が一番大きいのでANSWERは’７’になります。図12-02の1行目とピタリ一致していることを確認しましょう。 （＊２）FPGAの内部信号を観測できるツール。使い方はここ。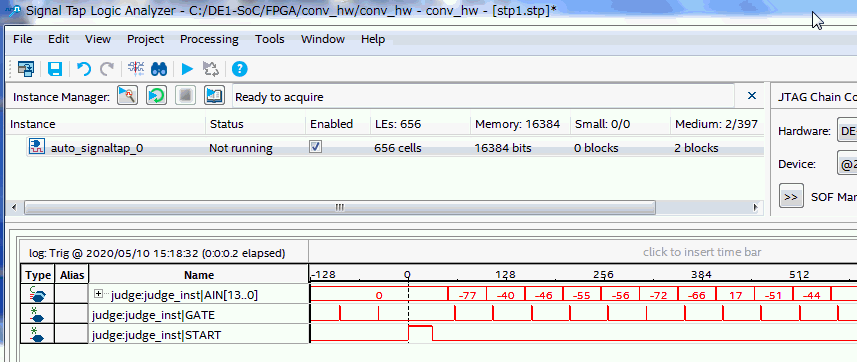 　　図12-03　MNISTの1枚目は数字の’７’ 　図12-04はAINの2＋１番目が一番大きいのでANSWERは’２’になります。図12-02の2行目とピタリ一致していることを確認しましょう。 　　図12-04　MNISTの2枚目は数字の’２’ 　図12-05はAINの1＋１番目が一番大きいのでANSWERは’１’になります。図12-02の3行目とピタリ一致していることを確認しましょう。 　　図12-05　MNISTの3枚目は数字の’１’ 　図12-06はAINの0＋１番目が一番大きいのでANSWERは’０’になります。図12-02の4行目とピタリ一致していることを確認しましょう。 　　図12-06　MNISTの4枚目は数字の’０’ 　図12-07はAINの4＋１番目が一番大きいのでANSWERは’４’になります。図12-02の5行目とピタリ一致していることを確認しましょう。 　　図12-07　MNISTの5枚目は数字の’４’ 　図12-08はAINの1＋１番目が一番大きいのでANSWERは’１’になります。図12-02の6行目とピタリ一致していることを確認しましょう。 　　図12-08　MNISTの6枚目は数字の’１’ 　図12-09はAINの4＋１番目が一番大きいのでANSWERは’４’になります。図12-02の7行目とピタリ一致していることを確認しましょう。 　　図12-09　MNISTの7枚目は数字の’４’ 　図12-10はAINの9＋１番目が一番大きいのでANSWERは’９’になります。図12-02の8行目とピタリ一致していることを確認しましょう。 　　図12-10　MNISTの8枚目は数字の’９’ 目次へ戻る