 FFTに関する情報はたくさんありますが、バタフライ演算の中で何が行われているかをベクターイメージを使って説明している書籍等はなかなか見つからないと思います。
FFT (Fast Fourier Transform)とはDFT (Discrete Fourier Transform)を高速化する上で非常に効果的な手法です。Fig.1は8ポイントFFTのブロックダイアグラムです。ここでの足し算や掛け算は複素演算であることに注意しましょう。
 |
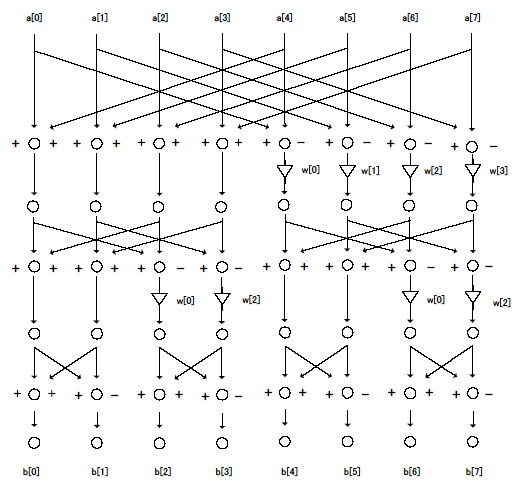| Fig.1この規則に従って計算する(Cooley-Tukeyｱﾙｺﾞﾘｽﾞﾑ) |
w[n]は回転因子"twiddle factors"と呼ばれます（Fig.2）。a[n]は時間軸データ"time-domain
data"です（Fig.3）。このケースではw[n]は複素数でa[n]は実数になります。
 |
 |
| Fig.2 この回転因子を使う |
Fig.3 時間軸データを入力 |
以下はベクターイメージによるFFTの説明です。そんじょそこらのFFT説明記事とは違って難しい数式は一切使用しません。是非ご一読ください！
ご質問、ご意見、ご指摘等がございましたらメールください。
| e-mail : |
iwata@digitalfilter.com |
|
|