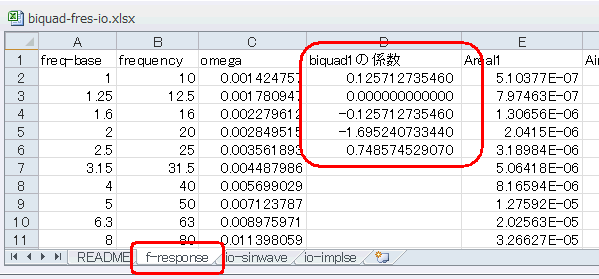
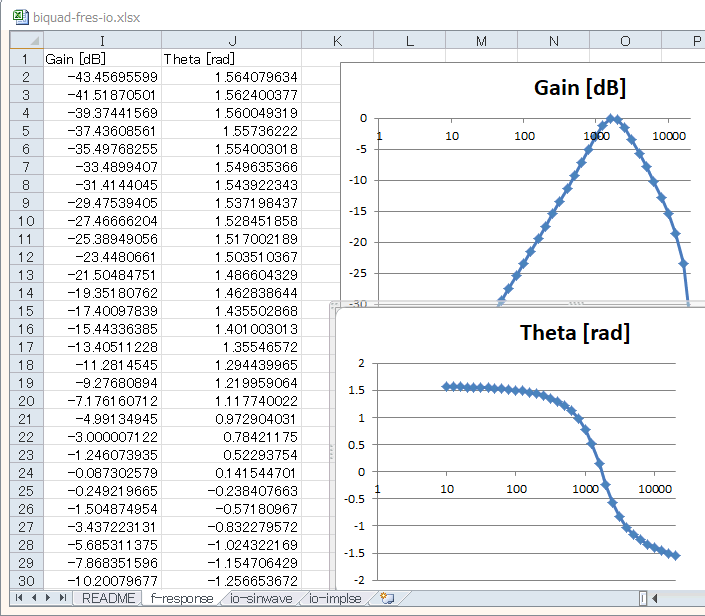
1-03　BPF/BRFの周波数・入出力特性 ●フィルタ係数を変えてBPFに 　今度は係数をBPF（Band Pass Filter, 帯域通過フィルタ）に変えてみます。これから係数をコピーして f-responseシートにペーストします（＊１） （＊１）他のシート（io-sinwave, io-impulseシート）の係数は自動的に更新される。 　図1-31　係数はこのシートで変える ●1k〜3kHzが通過、低域、高域は減衰 　図1‐32の上が振幅特性ですが、カットオフ1kHz/3kHzのBPFになっています。同図下は位相特性ですが、低域は正方向、高域は負方向に振れています。 　図1-32　BPFの特性。カットオフは1kHz/3kHz ●低い方のカットオフ1kHzを見てみる 　入力が1kHzの場合、出力は図1‐33のように、振幅は-3dB、位相は40度(0.7rad)ほど進みます（サイン波の山の位置が少し早くなっている）。図1‐32の周波数特性と比較してみましょう。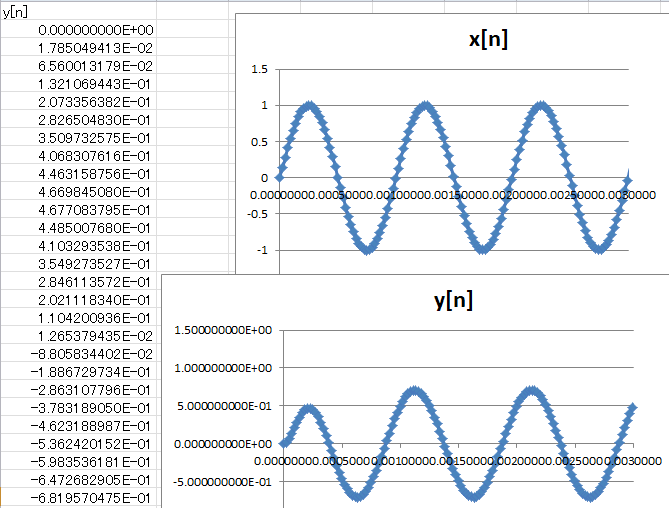 　図1-33　位相が進んでいる（立ち上がり、立ち下がりが早まる） ●2kHzはBPFの通過帯域 　入力が2kHzの場合、出力は図1‐34のように、振幅は減衰せず、位相も同じになります。図1‐32の周波数特性と比較してみましょう。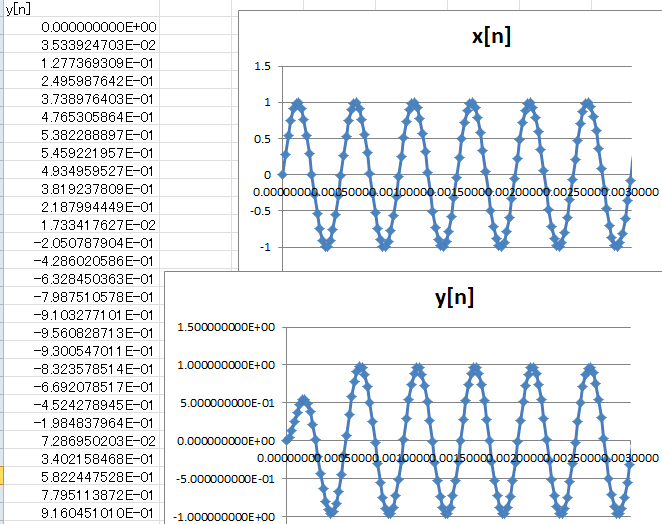 　図1-34　通過の中心周波数。減衰なし、位相も同じ ●高い方のカットオフ3kHzを見てみる 　入力が3kHzの場合、出力は図1‐35のように、振幅は-3dB、位相は40度(0.7rad)ほど遅れます（サイン波の山の位置が少し遅くなっている）。図1‐32の周波数特性と比較してみましょう。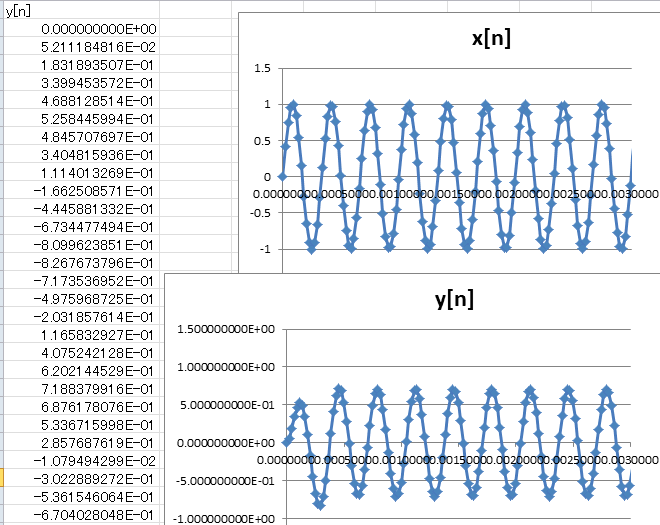 　図1-35　位相が遅れている ●io-impulseシートでインパルス応答 　BPFのインパルス応答は図1‐36のように直流分がなくなります。直流(0Hz)の減衰が深いのでこうなります。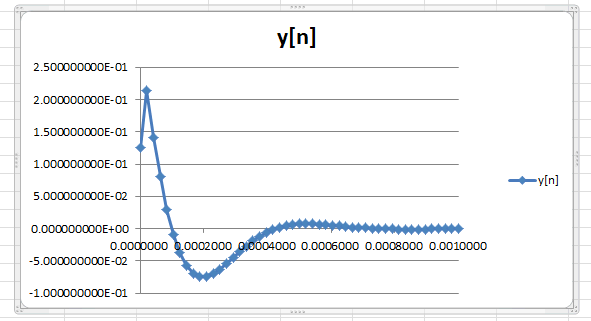 　図1-36　io-impulseシートでインパルス応答 次のページへ 目次へ戻る