5-01 1kHzのサイン波の自己相関を見る
●EXCELで自己相関を体感しよう!
信号解析の手法の一つとして「自己相関」があります。このExcelをダウンロードして開いてみましょう。最初のREADMEシート(図5‐01)にEXCELファイルの簡単な説明があります。
同図に自己相関関数の定義式があります(*1)。その式の下にあるように本EXCELではN=500,
M=45とします。
(*1)自己相関の定義には「x[i]からその平均値を引いてから積和」して、さらに「積和結果をNで割る」といった定義もあるが、それらは省略してある。 |
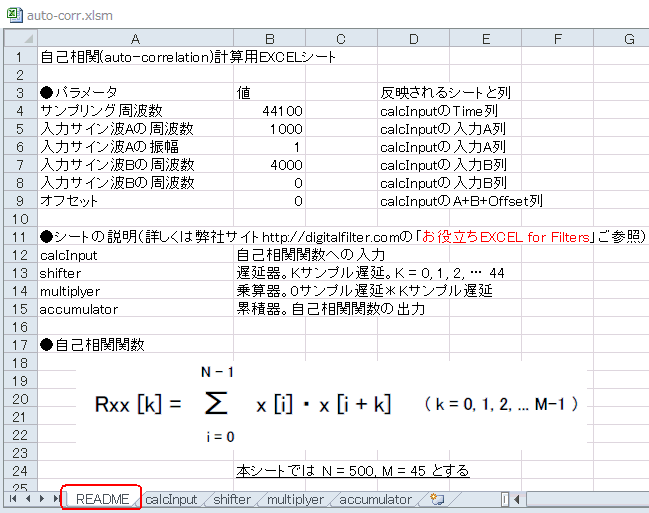
図5-01 最初のシートREADME
●隣のcalcInputシートを見る
自己相関関数への入力 x[i] はデフォルトで 1kHzのサイン波になります(図5‐02、calcInputシート)。サンプリング周波数が44.1kHzなので、同図のグラフのように約44サンプルで1周します。 |
図5-02 定義式における x[i] を計算するシート
●サイン波をkサンプルずらすシート
shifterシートでは x[i+k] の計算を行います。図5‐03のように例えばE列(k =
3)なら x[i+3] なので、図5‐02のサイン波 (x[i]) を3個ずらしたものになります(各セルをクリックすると計算式を見ることができる)。 |
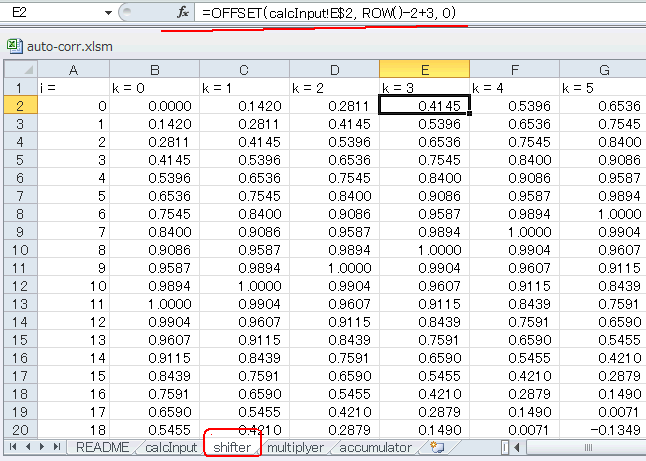
図5-03 B列は0サンプル、C列は1サンプル、D列は2サンプルとずらしていく
●サイン波どうしを掛け合わせるシート
multiplyerシートでは x[i] x[i+k] の乗算を行います。例えばE列 (k=3) ではshifterシートのB列
(k=0)とE列 (k=3) の乗算を行います(図5‐04のようにセルをクリックすると計算式を見れる)。 |
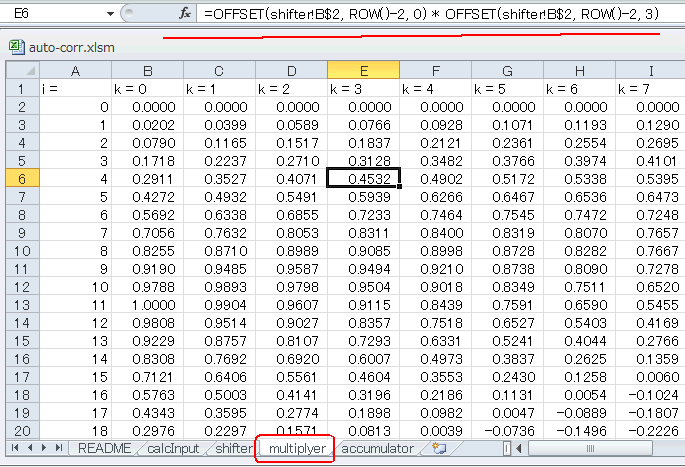
図5-04 各列500個の乗算結果がある
●各kにおいて乗算結果500個を加算して1個の結果を得る
accumulatorシートでは図5‐05のようにmultiplyerシートの各列を累積します。例えば k=3 のセルは図5‐04のE列を累積したものです。k は0〜44まであり、自己相関結果をグラフにすると同図のようになります。 |
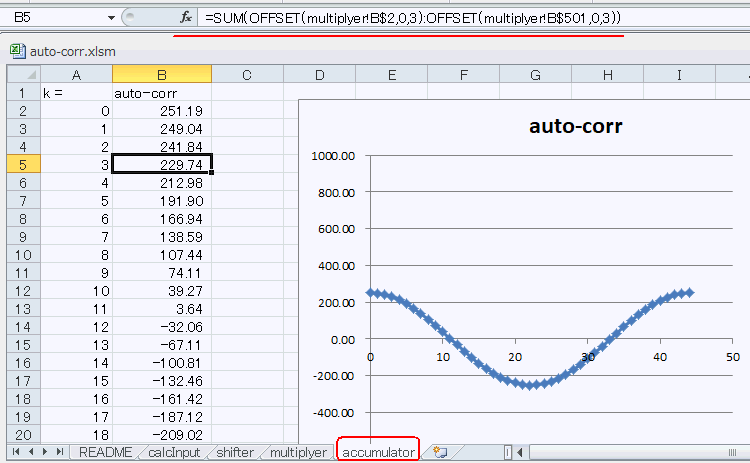
図5-05 k = 0, 44で極大、22で極小
●なぜこのような結果になるのか
入力が1kHz、サンプリングが44.1kHzなので約22サンプルでサイン波が反転します。したがってその位置
(k=22) の自己相関値は極小になります(*2)。
そして44サンプルずらすとサイン波は同相になり、符号が揃うため自己相関値は極大になります。
(*2)22サンプルずらすと x[i] と x[i+k] の符号が常に逆になる。44サンプルだと符号は常に同じになる。
本EXCELではM=44、すなわちk = 0, 1, 2... 44まで計算しますが、k=66 だとまた極小になり、k=88だとまた極大になることは容易に想像できます。このように自己相関値は周期が約44で波打つ関数になります。 |
次のページへ
目次へ戻る |









