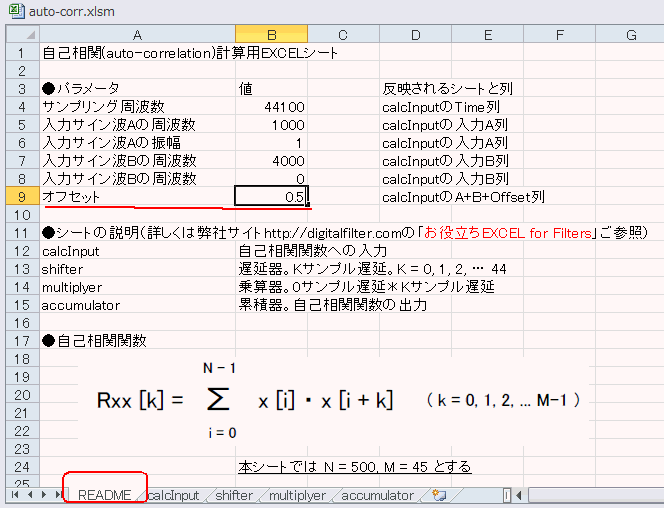
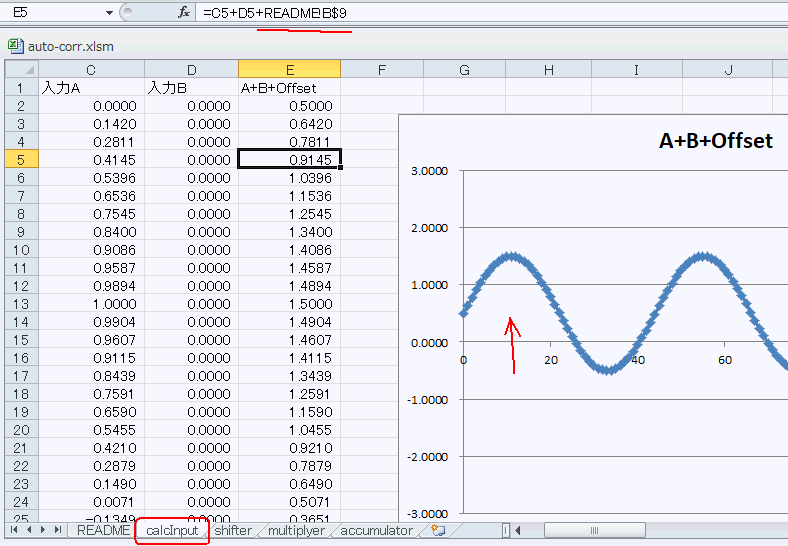
5-01　1kHzのサイン波の自己相関を見る（続き） ●自己相関におけるオフセットの影響 　デフォルトでは入力は1kHzのサイン波でしたが、もしオフセットがあったらどうなるでしょうか？READMEシートのB9セルを0.5としてみましょう（図5‐08）。 　　図5-08　B9セルでオフセット 0 -> 0.5 ●入力が正の方向に引っ張られる 　calcInputシートを見るとサイン波が少し上に上がっています（これと比較）。E列でオフセット(0.5)が加算されていることを確認しましょう（図5‐09）。 　　図5-09　自動的に入力が計算される ●出力も正方向に引っ張られる 　オフセット加算により、shifter、multiplyerシートでは正の値が多くなっています。それらを積和したものは当然正方向に引っ張られるので、accululatorシートは図5‐10のように少し上に上がります（これと比較）。B列を見ると全体的に125程度上がっています（＊１）。 （＊１）オフセットが0.5、N=500なので自己相関値は 0.5 x 0.5 x 500 = 125 アップする。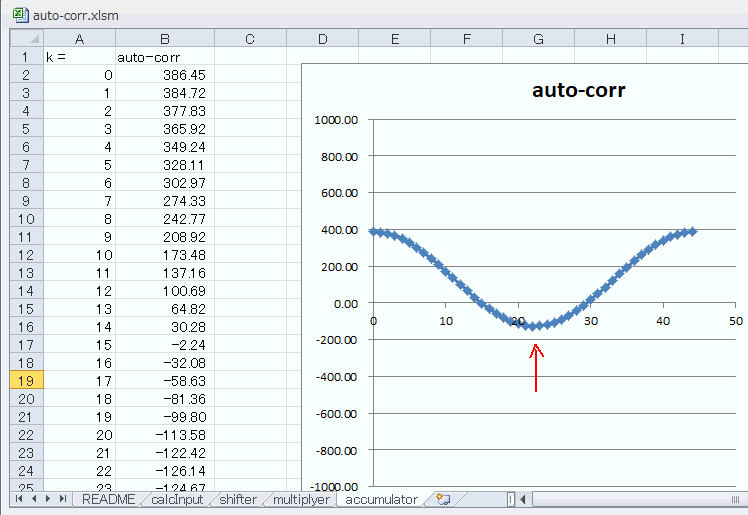 　　図5-10　自己相関の結果が自動的に計算される ●入力のオフセットが大きければ出力も大きくなる 　READMEシートに戻ってオフセットを1.2とするとさらに上がって図5‐11のようになります。1.2 x 1.2 x 500 = 720 ほど上がります。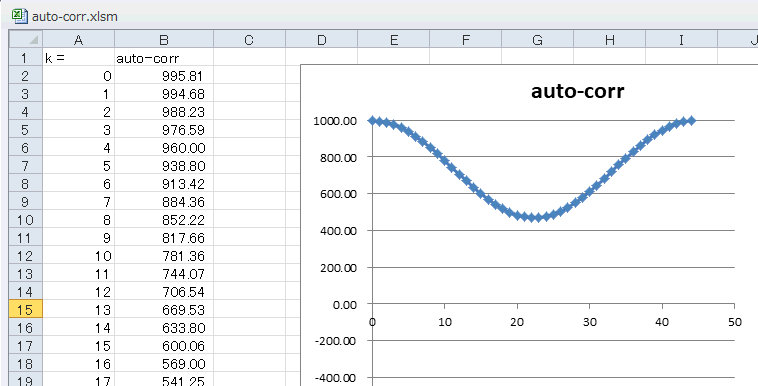 　　図5-11　自己相関値はすべて正の値になっている ●オフセット正／負で結果を比較しよう 　オフセットが負の値だったらどうなるでしょうか？図5‐12のように-1.2 としてみます。 　　図5-12　READMEシートでオフセットを変える ●オフセットが負の値でも大差ない 　結果は図5‐13のようになり、正のとき（図5‐11）と基本的に同じになります（＊２）。積和演算なので「正か／負か」ではなく、「符号が同じか／違うか」に依存するからです。 （＊２）サイン波の始まり方（絶対値が増えていく／減っていく）によって微妙に結果は変わる。calcInputのグラフ参照。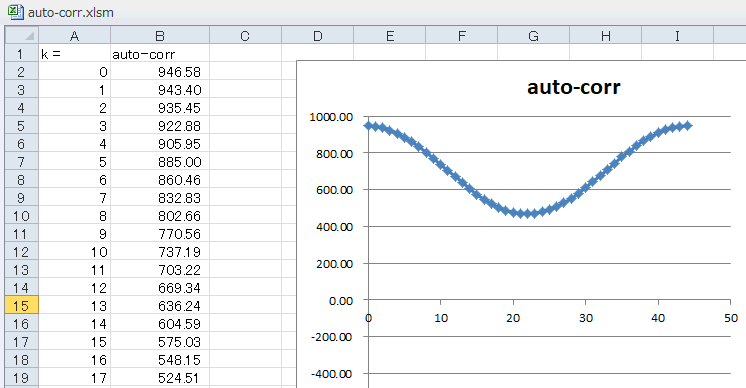 　　図5-13　オフセットを-1.2とした結果 ●周期信号の発見に使える自己相関 　自己相関値をとることにより、「周期信号を含むかどうか」が分かります。また「山と谷の差」や「山と谷の位置」により、その成分の周期や大きさが分かります。またオフセットがあっても、山と谷の差や位置は変わりません。 　本EXCELでは x[i] のシフト、x[i] x[i+k] の計算などをVBAで行います。N (=500)の値、M (=45)の値などを変更するにはVBAを変更すると良いでしょう。 最初のページへ 目次へ戻る