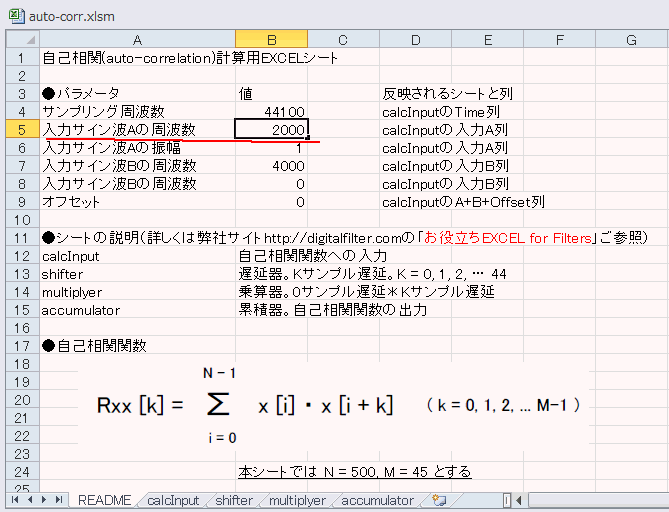
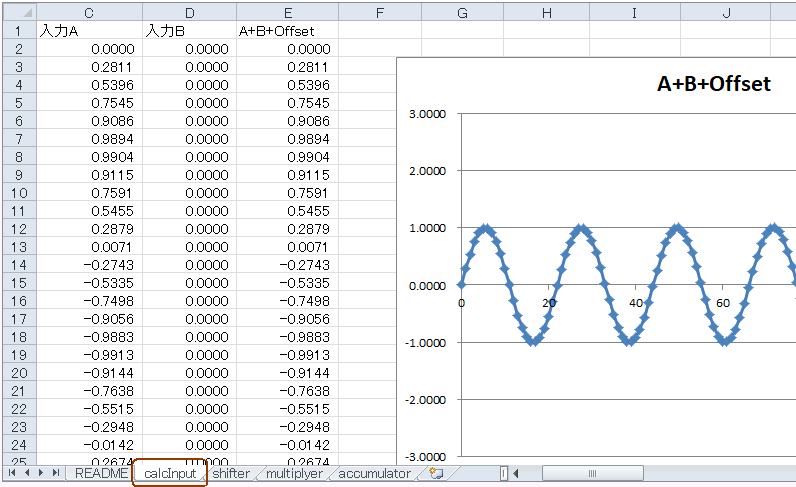
5-02　色々な信号の自己相関を見る ●入力周波数を速くしてみる 　前節では1kHzのサイン波の自己相関を見ましたが、2kHzだとどうなるでしょうか？図5‐18のようにREADMEシートを変更します。 　　図5-18　READMEシートのB5セルを1000→2000に ●すると入力が2kHzになる 　calcInputシートを見ると振動が速くなっています（図5‐19）。2kHz＠サンプリング44.1kHzなので、サイン波が約22サンプルで一周します。 　　図5-19　44.1kHz / 2kHz = 22サンプルで1周 ●自己相関値が自動的に計算される 　accululatorシートを見ると図5-20のように45サンプルで2周しています（1kHzでは1周）。入力の振動が2倍になると自己相関の振動も2倍になります（＊１）。 （＊１）約11サンプルで符号が反転して自己相関は極小、約22サンプルで符号が揃って自己相関は極大になる（図5‐19参照）。 　　図5-20　k=11で極小、k=22で極大・・・を繰り返す ●もっと入力を速くする 　READMEシートに戻って入力を3000にしてみましょう（図5‐21）。入力が3kHzのサイン波になります。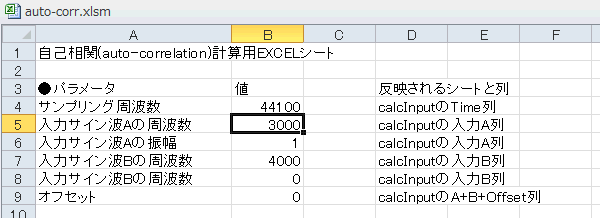 　　図5-21　B5セルを3000に ●自己相関値もさらに速く振動する 　accumulatorシートを見ると45サンプルで3周しています（図5‐22）。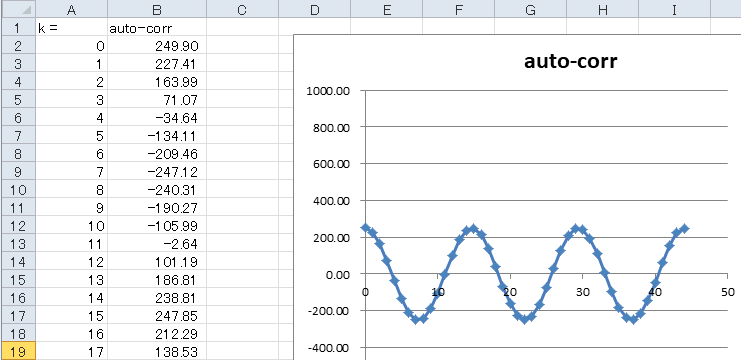 　　図5-22　44.1kHz / 3kHz = 15サンプルで1周 ●4kHz＠サンプリング44.1kHzの自己相関値 　入力を4kHzにすると自己相関値は45サンプルで4周します（約11サンプルで1周）。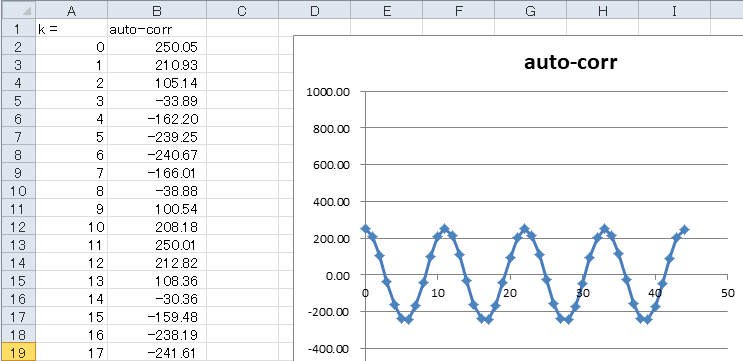 　　図5-23　44.1kHz / 4kHz = 11サンプルで1周 ●自己相関をとることにより分かること 　このように自己相関値の山と谷の間隔を見ると周期信号の周波数が分かります。また山と谷の差を見るとその振幅もわかります（＊２）。 （＊２）フーリエ解析の「簡易版」といったところでしょうか。自己相関はDFTと比べると乗算数は少なくなりますが、FFTと比べるとそれほど変わらない、あるいはちょっと多いかなという印象です。 次のページへ 目次へ戻る