5-03 複合周波数信号の自己関数を見る(続き)
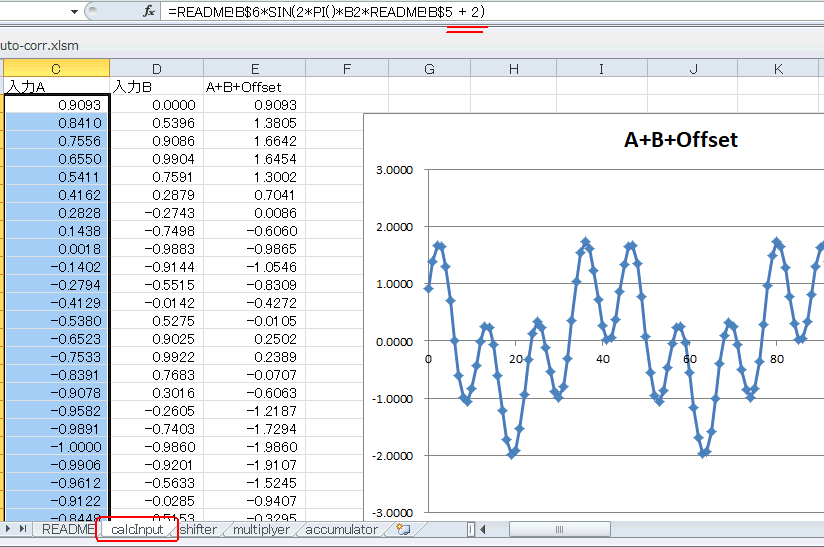 図5-41 位相をずらして自己相関をとる
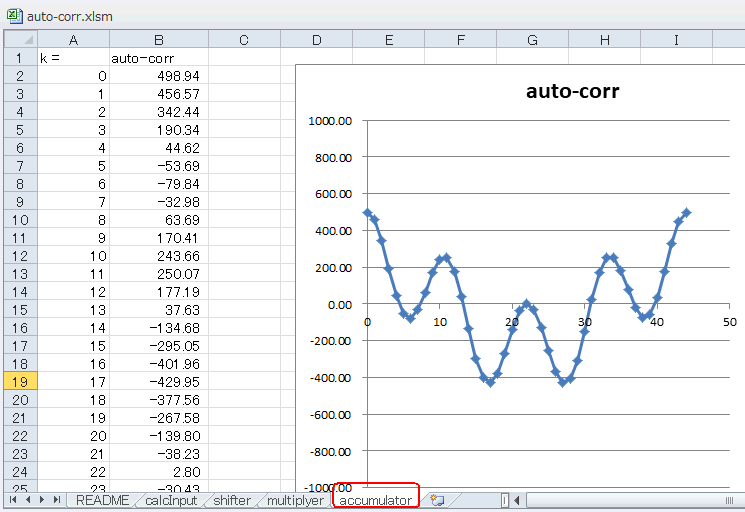 図5-42 位相と自己相関値は関係なさそう
 図5-43 かなりノイジーな1kHz
 図5-44 ノイズがあっても自己相関値はそれほど変わらない
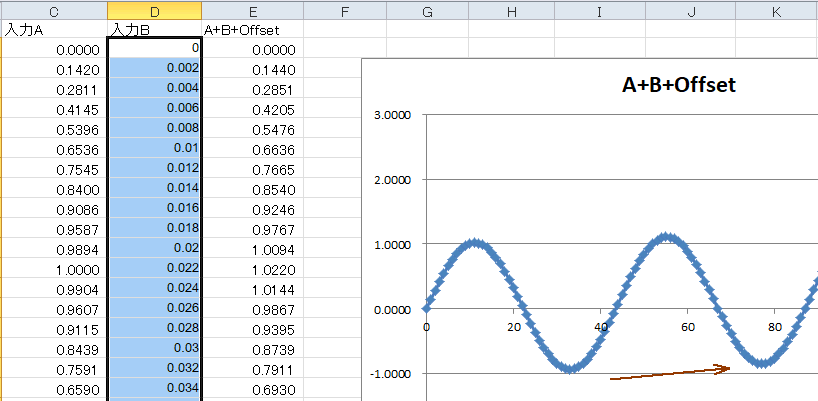 図5-45 サイン波が徐々に持ち上がっていく
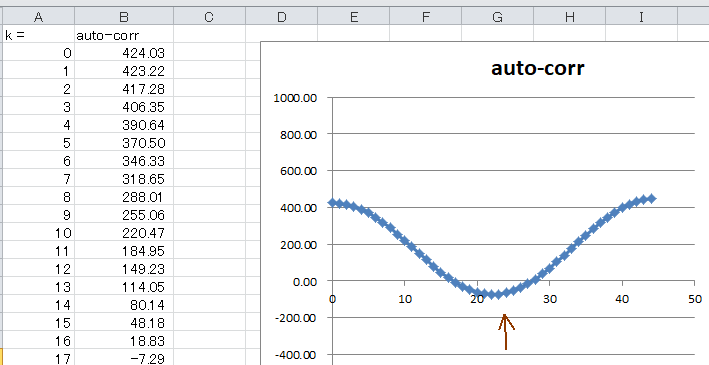 図5-46 バイアスのぶん自己相関値が上がる 最初のページへ 目次へ戻る |
||||||||||||||||||||||||
5-03 複合周波数信号の自己関数を見る(続き)
 図5-41 位相をずらして自己相関をとる
 図5-42 位相と自己相関値は関係なさそう
 図5-43 かなりノイジーな1kHz
 図5-44 ノイズがあっても自己相関値はそれほど変わらない
 図5-45 サイン波が徐々に持ち上がっていく
 図5-46 バイアスのぶん自己相関値が上がる 最初のページへ 目次へ戻る |
||||||||||||||||||||||||