5-03 複合周波数信号の自己関数を見る
●入力1000Hz+4000Hzだとどうなるか
それでは複数の信号をミックスして見ましょう。図5‐36のように入力Bの周波数を4000、振幅を1.0としてみましょう。 |

図5-36 入力Bの振幅を0から1にする
●加算結果はE列
calcInputシートを見ると図5‐37のように1kHzと4kHzがミックスされています。 |
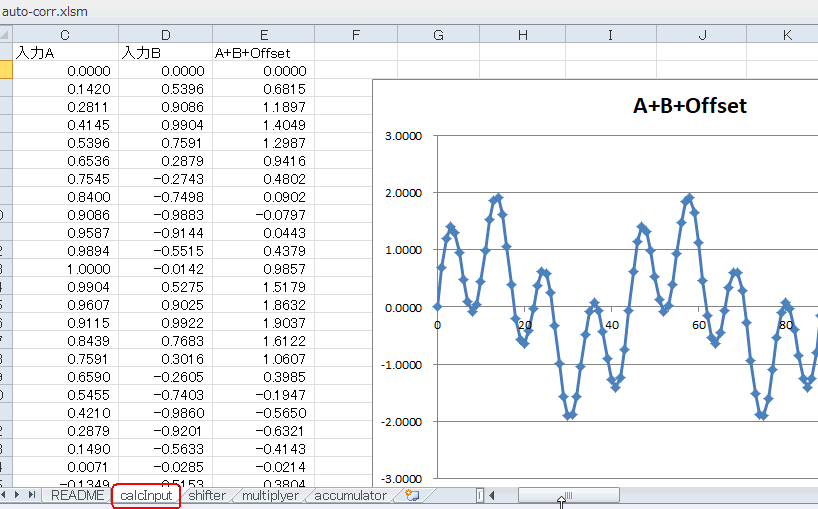
図5-37 44サンプルで1周する成分と4周する成分
●自己相関値もミックスされる
accumulatorシートを見ると自己相関値は、「44サンプルで1周」+「44サンプルで4周」の成分になっています(図5‐38)。これとこれがミックスされた形です。 |
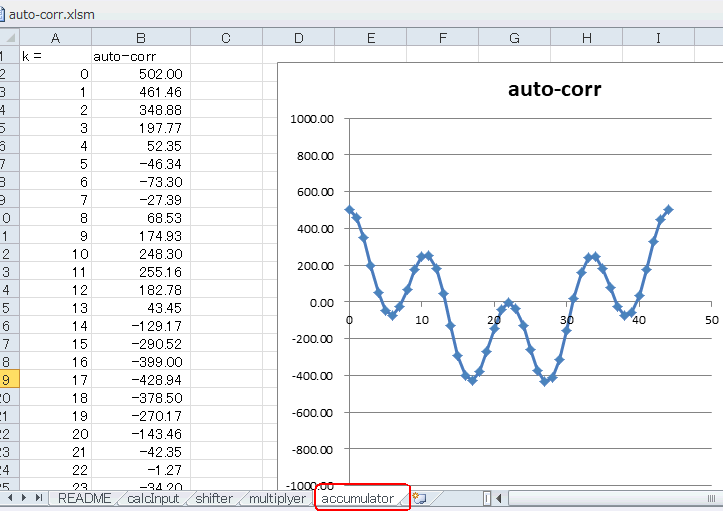
図5-38 自己相関値も1kHz+4kHz
このように、2つのサイン波がミックスされても「自己相関」をとることにより、それらの周波数や振幅を判別できます。
ただし、3つ、4つ、5つとミックスされると、さすがに個々のサイン波の判別は難しくなります。そのような場合は「フーリエ解析」の出番になると思います。
●自己相関値と位相の関係は…
ここで1kHzの位相をずらしてみましょう。図5‐39のようにC2セルに"+2"として下まで引っ張ります(*1)。
(*1)単位はラジアンなので 2 x 180 / PI = 115度、位相を進める |
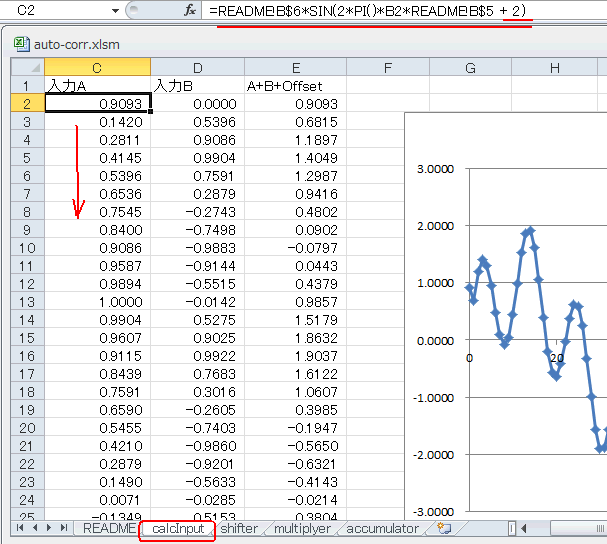
図5-39 入力Aの計算式に2[rad]を加えて下まで引っ張る
次のページへ
目次へ戻る |







