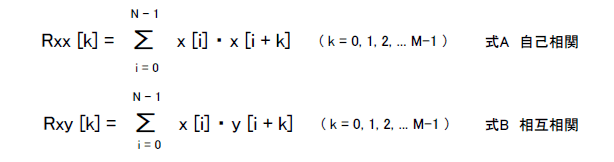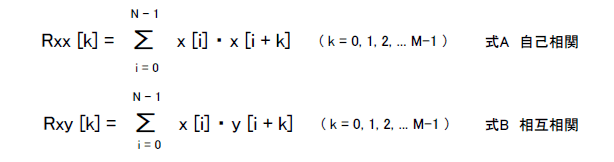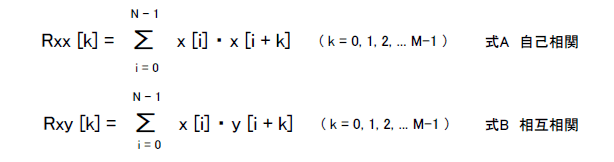
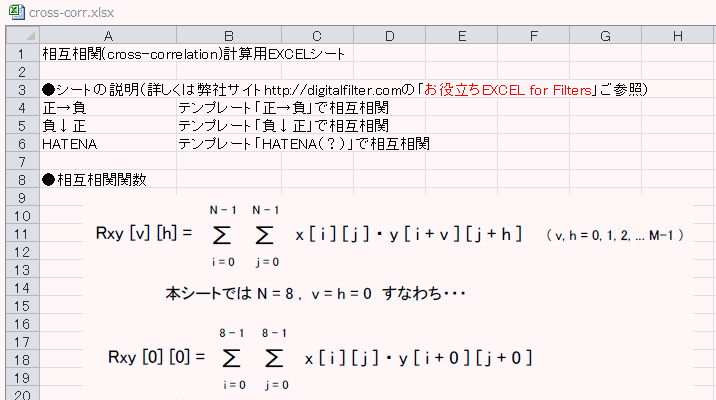
5-04　相互相関を画像に適用する ●相互相関（一次元）の定義 　自己相関関数は下記式Aであるのに対し、本章で扱う相互相関関数は式Bになります。このように相互相関 Rxyは x, y という2つの数列の積和からなります。 ●相互相関を二次元に拡張する 　このExcelをダウンロードして開いてみましょう。最初のREADMEシート（図5-51）にEXCELファイルの簡単な説明があります。 　上記式Bは「一次元」の相互相関でしたが、同図ではそれを「二次元」に拡張してあります（＊１）。 （＊１）式Bにおけるx, yは「配列」だが、図5‐51におけるx, yは「行列」になる。 　また同図にあるようにここでは N = 8, v = h = 0 としています。すなわちx, yは8x8の行列、相互相関の結果はRxy[0][0]の一つになります。 　　図5-51　最初のシートREADME ●二次元、すなわち画像同士の相関 　READMEシートの下の方にx, yの形状があります。どちらも8×8で、xの方を「テンプレート」、yの方を「対象画像」と呼びます。本EXCELでは、xは3種類、yは9種類用意し、これらを組み合わせた相互相関値を吟味します。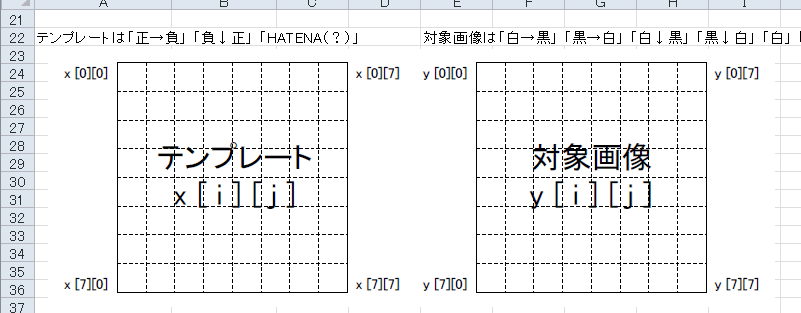 　　図5-52　READMEシートの下の方 ●最初のテンプレート 　隣の「正→負」のシートを見るとA〜H列に8×8の「テンプレート」があります。図5‐53では左半分は+1、右半分は-1になっています（値が正→負になっている）。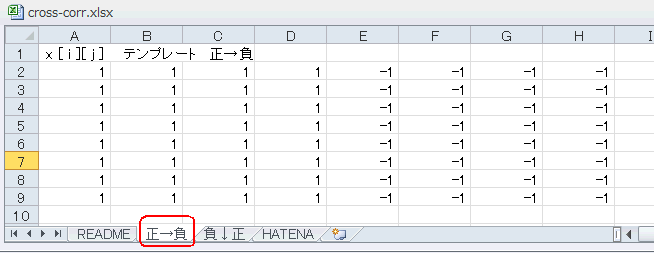 　　図5-53　+1が32個、-1が32個、計64個 ●最初の対象画像 　同シートのJ〜Q列には「対象画像」があります。図5‐54では右に行くにつれて値が小さくなっています（白→黒）。グラデーションがかかっており、40は「白い画素」、5は「黒い画素」という意味です。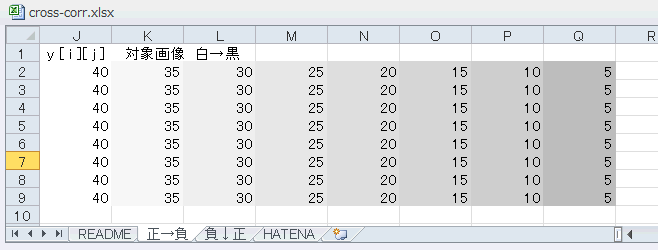 　　図5-54　対象画像も8×8＝64画素ある ●相互相関の式（図5‐51）の乗算の部分 　同シートのS〜Z列（図5‐55）はテンプレートと対象画像の各画素を乗算したものです（各セルをクリックすると計算式を見ることができる）。同図の右半分が負の数なのはテンプレートの右半分が"-1"だからです。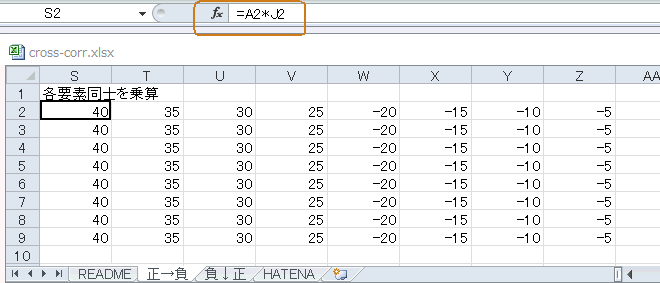 　　図5-55　左半分は1倍、右半分は‐1倍 ●相互相関のの式（図5‐51）の累積の部分 　8×8の乗算結果（上図）をすべて足し合わせた結果（相互相関値）は同シートの右端、AB列にあります。上図では正の値が支配的になっているので、これらを足し込むと図5‐56のように"640"という正の大きな値になります。 　　図5-56　テンプレートと対象画像の相関が強いということ 次のページへ 目次へ戻る