4-01 DFTとFFT〜乗算の数を比較してみよう
●EXCELでフーリエ変換は出来ない!?
まずはこのマンガを読んでみてください。
ひとまず「フーリエ変換」を理解したとします。それでは実際にパソコンで計算してみよう・・・あれっ?積分のプログラムってどう書くんだっけ?・・・いわゆる「アナログ版フーリエ変換」ではここで思考停止してしまいます。
そこで考えられたのがDFT(Discrete Fourier Transform)です。このExcelをダウンロードして開いてみましょう。最初のREADMEシート(図4‐01)にEXCELファイルの簡単な説明があります。 |
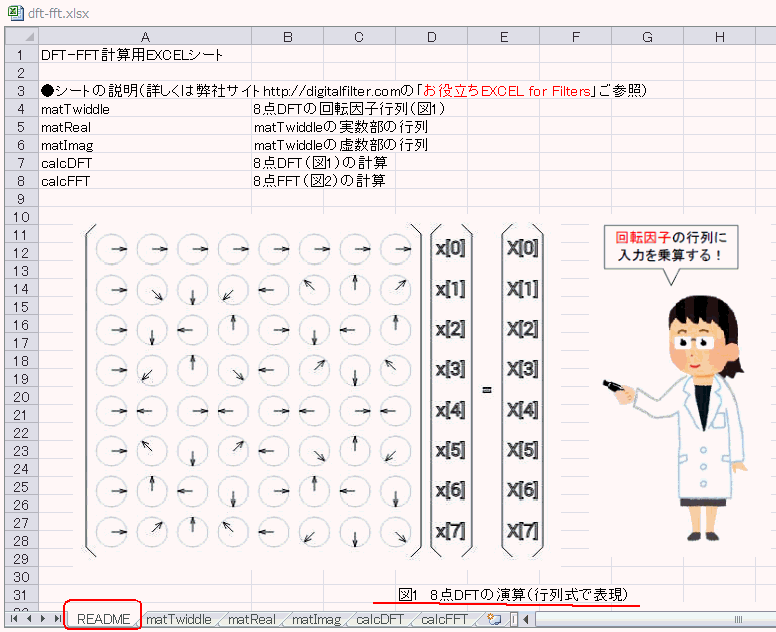
図4-01 最初のシートREADME
●DFTならEXCELで計算できる!
このEXCELでは「8点DFT」を行います。READMEの図にあるように、8点の入力 x[n] に 8×8の「回転因子行列」を乗算すると8点の出力 X[k] が得られます。
回転因子行列はこのような複素ベクトルからなります。8ステップで単位円を一周、8点DFTならこの8種類のみになります。
回転因子はmatTwiddleシートで生成します。図4‐02のように、IMEXP関数の引数に複素数の実数部、虚数部を入れ、ROW、COLUMNに応じて角度を変えることにより図4‐01のような行列を生成します。 |
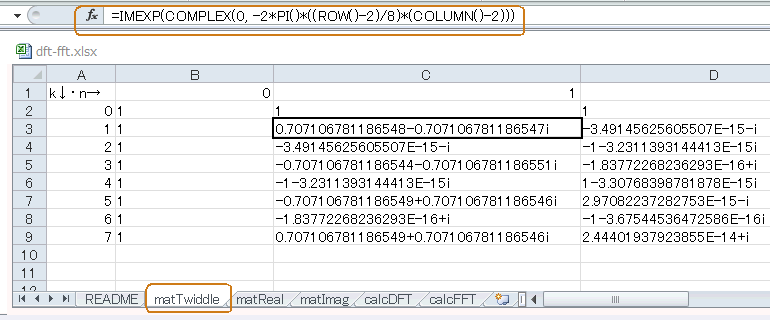
図4-02 回転因子行列を計算するmatTwiddleシート
●回転因子行列を実数部、虚数部に分ける
matTwiddleシートで生成する値は複素数ですが(*1)、見やすく・計算しやすくするために実数部と虚数部を分離します。
図4‐03(a)のようにmatRealシートにその実数部、同図(b)のようにmatImagシートにその虚数部を置きます。
(*1)IMEXP関数の出力は複素数だが「文字列」なので桁数を調整することができない。IMREAL/IMAGINARY関数で分離して数値化する。 |
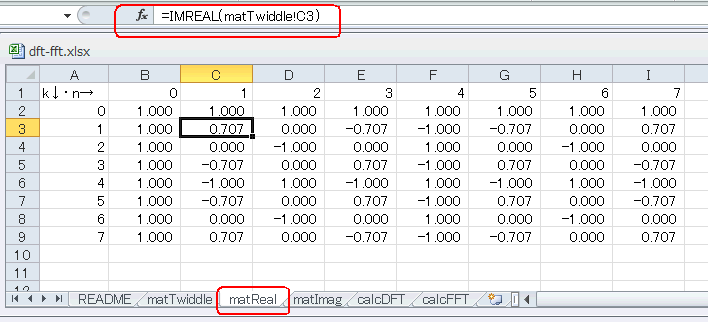 (a) (a)
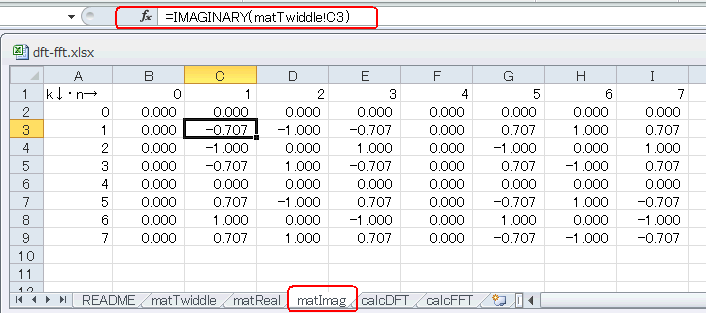 (b) (b)
図4-03 matRealシートに実数部、matImagシートに虚数部
●実数部と虚数部を別々に行列乗算
calcDFTシートではDFTを計算します。入力はx[0]〜x[7]の8点の実数、出力はX[0]〜X[7]の8点の複素数になります。
行列乗算は図4‐04のようになり、実数部に8回、虚数部にも8回の乗算が必要になります。出力は複素数なので、1点計算するのに16回の乗算、8点計算するのに128回の乗算を行います。 |

図4-04 各セルをクリックして演算を見てみる
●DFTの点数が多いと大変なことに…
N点DFTでは(N^2)*2回の乗算が必要になります。DFTの点数は一般的に1024以上になることが多く、表4‐01に示すように多量の乗算が必要になり、演算に時間がかかるようになります。 |
| DFTの点数 |
乗算の数 |
| 8 |
128 |
| 16 |
512 |
| 64 |
8,192 |
| 256 |
131,072 |
| 1024 |
2,097,152 |
| 4096 |
33,554,432 |
表4‐01 乗算は加算よりも時間がかかるのでその数に注意
●次のページでFFTを説明します!
そこで考えられたのがFFTです(図4‐05、READMEシートの下の方)。このようなバタフライ演算により乗算数が劇的に減少し(*2)、フーリエ変換ががより現実的になります。
(*2)なぜこのようなフローになるのかはこのサイト参照(スマホアプリで説明)。
それではcalcFFTシートを見てみましょう。 |

図4-05 8点の場合、3つのステージでFFT完成
次のページへ
目次へ戻る |


 (a)
(a) (b)
(b)



 (a)
(a) (b)
(b)
