コラム15　FFTをC言語で書くとこうなる 　図1-81, 82はFftCal関数の部分で、これにより1024点FFTが実行されます。 　図1-81　FftCal関数の一部。バタフライ演算の前処理 ●FFTには三角関数が必要なので値を配列に入れる 　図1-81の窓関数に関しては漫画14とコラム17で述べます。 　triという配列に三角関数の値を格納します。前半の512個はcos(0〜π)、後半の512個はsin(π〜2π)が入ります。 ●入力は実数のみ。ビット逆順で値を入れる 　fReal(実数が入る配列)には入力信号に窓関数を乗算したものを渡します。fImag(虚数が入る配列)はゼロで埋めます。 　その後fRealの要素を並び替えます(ビット逆順ソート)。なぜそうするかは表1-2を参照してください。 ●1024点FFTのステージは10ある 　その後は図1-82のようにバタフライ演算に入ります。一番外側のループ(変数i)は図1-75における「ステージ」に相当します。同図は8点FFTなので3ステージ(2点→4点→8点DFTと3段階）ですが、このプログラムは1024点FFTなので10ステージあることになります(2^10 = 1024なので)。 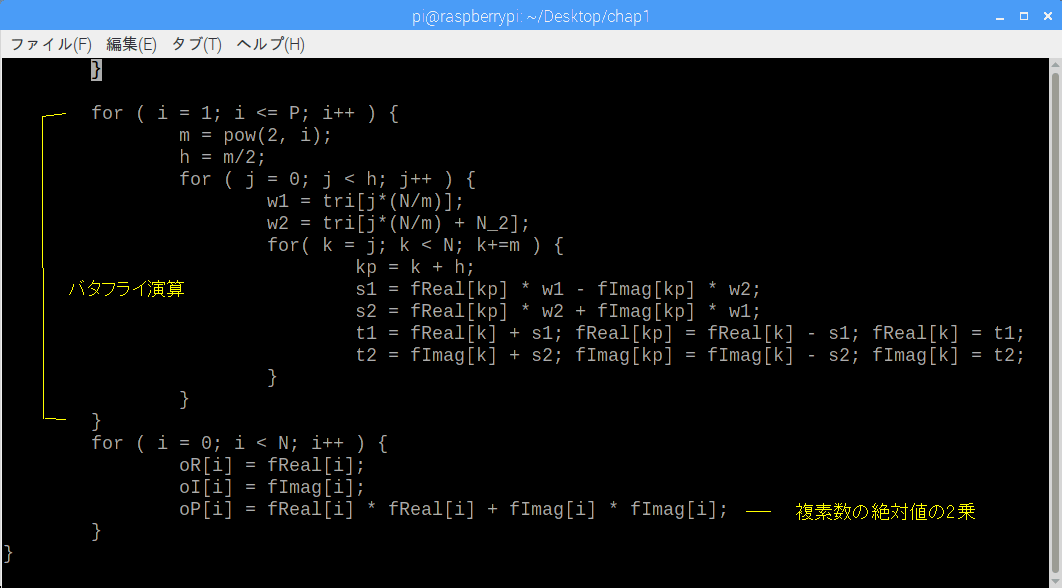　図1-82　バタフライ演算の部分 ●前もってビット逆順にしておけば後が楽になる 　図1-75では上からx[0], x[4], x[2], x[6], x[1], x[5], x[3], x[7]と並んでいますが、前もって「ビット逆順ソート」しているため、このプログラム内ではx[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7]...と並んでいると考えてください。 ●ステージが進むにしたがって「バタフライの羽」が長くなる 　最初のステージ(i = 1)ではx[0]とx[1], x[2]とx[3]といった、隣り合ったインデックスを読み出して複素乗算、加算が行われます。 　2番目のステージ(i = 2)ではx[0]とx[2], x[4]とx[6]といった、2つ離れたインデックスを読み出して複素乗算、加算が行われます。 　3番目のステージ(i = 3)では4つ離れたインデックスを読み出して複素乗算、加算が行われます。この辺りは図1-75の「バタフライの羽」の長さからイメージできると思います。 ●入力は実数のみだが出力は実数と虚数、どちらも値を持つ 　4番目のステージ(i = 4)では8つ離れたインデックス、・・・そして10番目のステージ(i = 10)では512個離れたインデックスを読み出して複素乗算、加算が行われ、1024点FFTは終了します。 　スペクトルは複素数であり、終了時にはfRealに実数部が、fImagの虚数部が入っています。 　oPには複素数の絶対値の2乗値が入り、対数をとった後、cvLine（OpenCVの関数）で描画します。 目次へ戻る