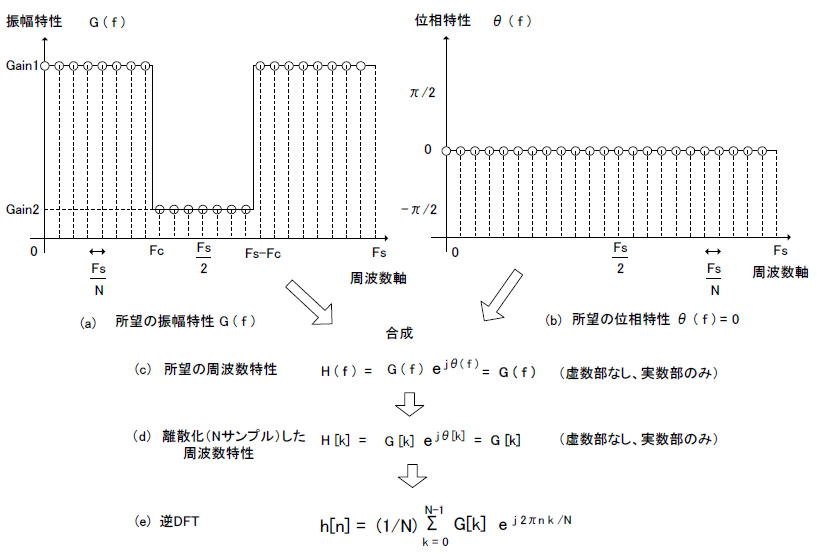
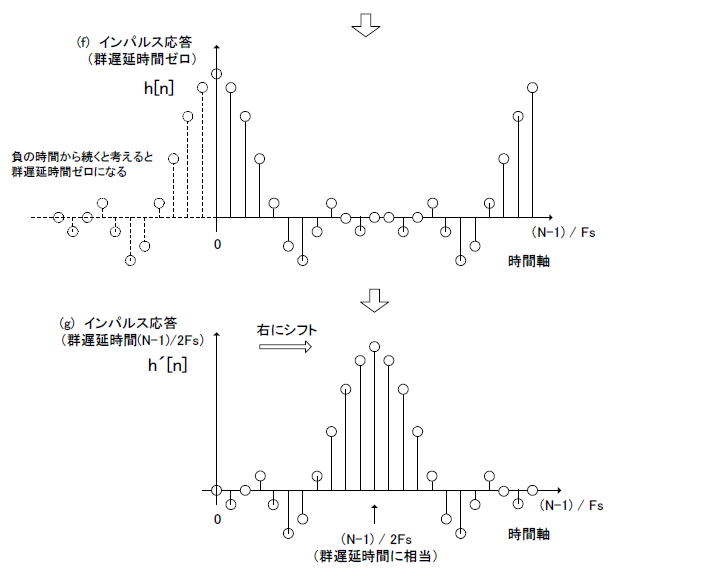
■手順2:位相特性を与えない、所望の振幅特性だけを与える係数導出法 実際の係数導出法として図2-78に「所望の位相特性を与えない方法」を示します。この方法では位相特性を「常にゼロ」(同図(b))としています。その結果、周波数特性は振幅特性のみとなり、常に実数になります(図2-78(c))。その後、周波数特性を離散化し(同図(d))、逆DFTを行います(同図(e))。 ●インパルス応答の中心の時刻はゼロになる 前節で述べたように「インパルス応答の中心」は「群遅延時間」を表します。逆DFTで得られたインパルス応答h[n]は図2-78(f)となり、その中心は時刻0、すなわち群遅延時間がゼロになっています。同図(b)において位相特性を常にゼロとしているので位相は遅れません。したがって群遅延時間はゼロになります。 ●群遅延時間ゼロのFIRフィルタの係数が得られる 「群遅延時間がゼロなんてあり得るの?」と疑問に思うかもしれませんが、図2-78(f)のようにインパルス応答が負の時間から続くと考え、そのようなFIRフィルタを実行したと考えてください。 ●群遅延時間を与えて終了 最後にインパルス応答を群遅延時間分、(N-1)/2Fs 右にシフトし h'[n] として終了です(図2-78(g))。この際新しいインパルス応答には左半分((N-1)/2Fsから左の部分)がないので、それを構築するために同図(f)の右半分を持ってきてもよいですし、インパルス応答の対称性を考えれば、コピーして左右折り返しても等価になります。 ●位相特性の決定は最後に行う このように位相特性を「常にゼロ」とおき、周波数特性の離散化、逆DFT、その後インパルス応答のシフト、と行えば所望の振幅特性に対するFIRフィルタの係数が求められます。FIRフィルタは直線位相特性を前提とされており、その位相特性の傾きは群遅延時間(一定)を意味します。すなわち「インパルス応答のシフト」は「位相特性の決定」と等価であるといえます。
●HPF, BPF, BRFの係数導出法 図2-78ではLPFに関して説明していますが、HPF(High Pass Filter、高域通過型フィルタ)、BPF(Band Pass Filter、帯域通過型フィルタ)、BRF(Band Reject Filter、帯域除去型フィルタ)については「次のページへ」をクリックしましょう。 次のページへ 目次へ戻る |