コラム2H　２次IIRフィルタの安定性 ●IIRフィルタの次数が増えたときの安定性は？ 　1次IIRフィルタの場合、このように極の絶対値が１より小さいかどうかで安定／不安定が決まります。それでは2次IIRフィルタだとどうなるでしょうか？分母が多次式になると、極の値が複素数になる場合があるので少し複雑になります。 ●極が実数、虚数、複素数に関わらず絶対値で決まる 　厳密な証明は他著に譲りますが、多次のIIRフィルタの安定条件は図2-180のようになります。すなわち、 「システムが安定であるためにはその伝達関数の極がすべて複素平面上の単位円内に存在しなければならない」 　またこれは十分条件でもあり、次も成立します。 「あるシステムの伝達関数の極がすべて複素平面上の単位円内に存在すれば、そのシステムは安定である」 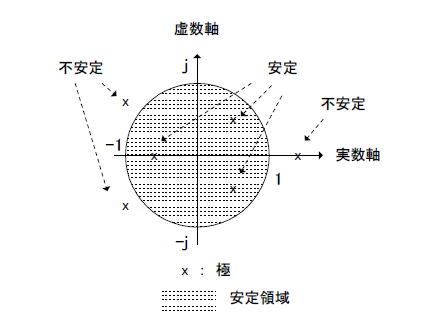　　　図2-180　IIRフィルタの極と安定領域 ●スマホアプリでインパルス応答が収束するか発散するかを見てみよう 　スマホアプリでは「2次IIRフィルタの安定性」を見ることもできます。「極が実数の場合と複素数の場合」、「極の実数部が正の場合と負の場合」、「絶対値が１以上の場合と１以下の場合」といった条件でインパルス応答を吟味できます。 �@ModeボタンでImpulseを選択するとインパルス応答が、Poleをクリックすると極分布が、F-Responseをクリックすると周波数特性が描画されます。 �Aテキストボックス内の係数値を適当に変更し、「Get Res」ボタンをクリックすると、それらの係数に対する特性が新たに計算されます。 �BGainボタンで周波数特性のレンジが変更できます。 ●安定なシステムとと不安定なシステムの例 　図2-181は「複素数」→「実数部負」→「絶対値1以下」の場合です。速く振動しながら減衰します。（安定） 　　図2-181　「複素数」→「実数部負」→「絶対値1以下」 　図2-182は「複素数」→「実数部正」→「絶対値1以上」の場合です。ゆっくり振動しながら発散します。（不安定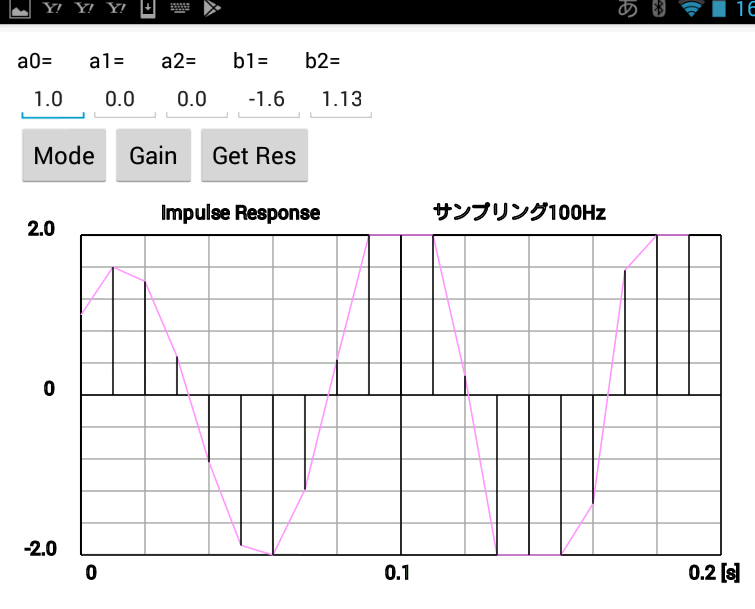） 　　図2-182　「複素数」→「実数部正」→「絶対値1以上」 ■ここでクイズ２つ！ ●クイズ１ 　極が純虚数の場合、インパルス応答が振動するのを証明しましょう。 ●クイズ２ 　極が複素数の場合インパルス応答は振動しますが、極の実数部の正･負でその振動周波数はどう変わるでしょうか。 クイズの答えはここ！ 目次へ戻る