●クイズ1の答え 　スマホアプリで「虚数」→「実数部なし」→「絶対値1以下」をクリックすると図2-183のようになります。 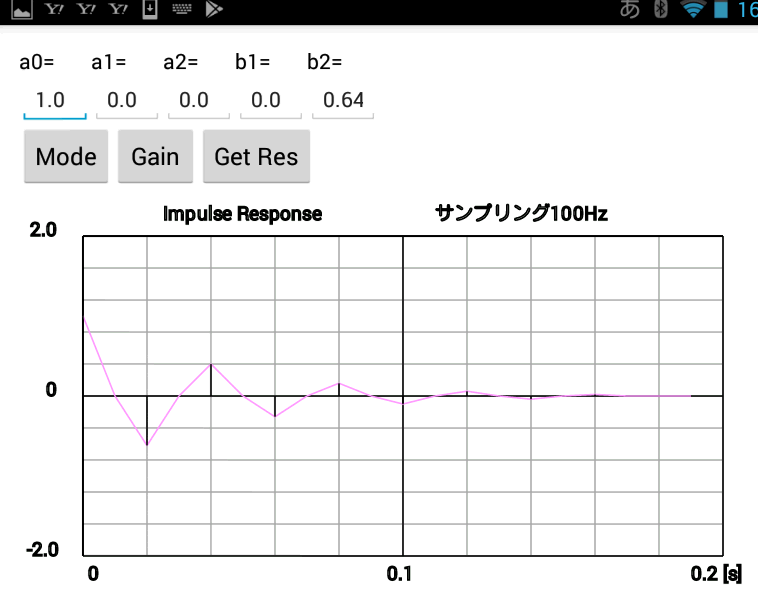　　図2-183　「虚数」→「実数部なし」→「絶対値1以下」 　図2-183ではインパルス応答が振動しています。この場合の伝達関数H(z)は、 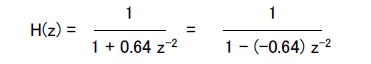式2-63 　上式を無限等比級数の和と考えて展開するとタップ数無限大のFIR型に変形できます。 式2-64 　したがってこのフィルタのインパルス応答は次のようになります。 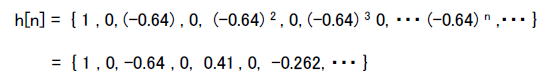式2-65 　このように極が純虚数の場合はサンプリング周波数の1/4の周波数で振動します。ただしこの場合振動はしますが、極の絶対値が1以下であり、インパルス応答がゼロに収束するため、このフィルタは安定です。すなわち極が純虚数の場合でもその絶対値が1以下なら安定、1以上なら不安定になります。 ●クイズ２の答え 　例えば「複素数」→「実数部正」→「絶対値1以下」をタップすると図2-184のようなインパルス応答が現れます。 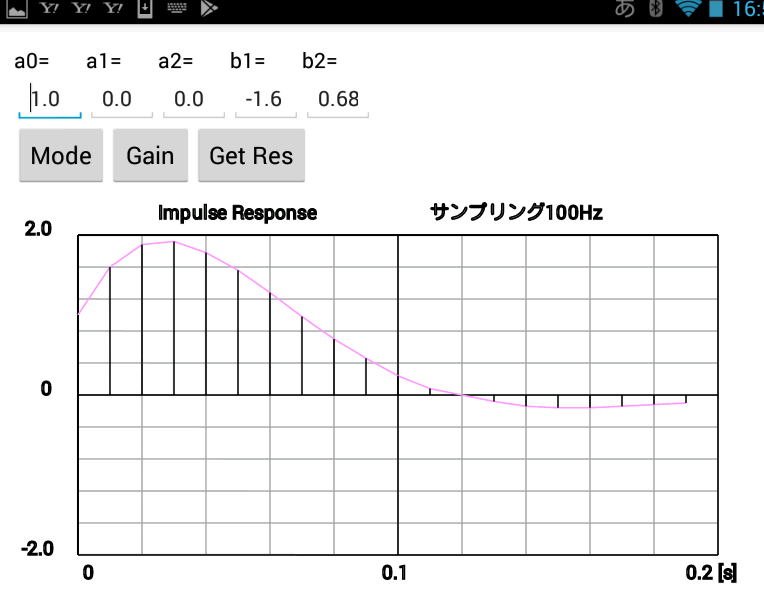　　図2-184　「複素数」→「実数部正」→「絶対値1以下」 ●極が複素数の場合のインパルス応答を計算する 　H(z)の分子が1で分母が2次式の場合、伝達関数は式2-66のように表されます。ここでp, qは極であり、この例ではp = 0.8 + j0.2, q = 0.8 - j0.2 になります（共益複素数）。 式2-66 　上式を部分分数展開すると、 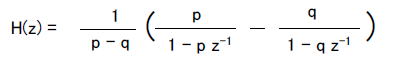式2-67 　上式を無限等比級数の和と考えて展開するとタップ数無限大のFIR型に変形できます。 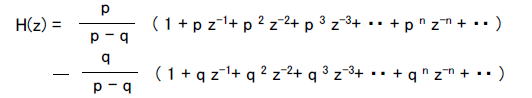式2-68 　するとインパルス応答は、 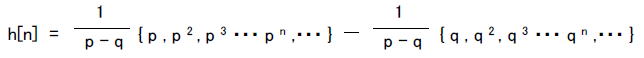式2-69 　pとqは共役複素数であることを鑑み、次のように変形すると、 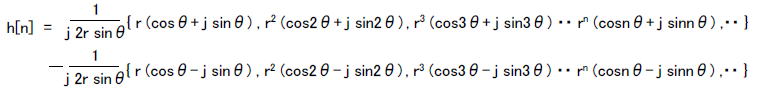式2-70 式2-71 　上式を整理すると次のような実数の数列になります。 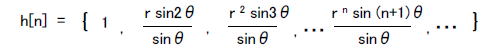　式2-72 　このように極が複素数の場合、インパルス応答は振動します。そして式2-72から分かるように、その振動周波数はθが小さい（実数部が正）場合は遅く、θが大きい（実数部が負）場合は速くなります。 　また、rが1以下の場合、このインパルス応答は安定であり、振動しながら減衰します。すなわち極が複素数でも、その絶対値が１以下なら安定、１以上なら不安定です。 前のページへ戻る 目次へ戻る