■サンプリング定理B (十分条件)
●一度細切れにしてしまった信号がちゃんと元に戻るのか?
前節でサンプリングにおける「必要条件」を説明しました。それでは「十分条件」はどうなるでしょうか?すなわち、
「原信号の最高周波数の2倍以上でサンプリングすれば、原信号を完全に復元できる」
は成立するのでしょうか?
結論から言うと成立します。しかしそのためには「ナイキスト周波数以上を完全にカットするアナログLPF」を施す必要があります。
●パルス状に離散化された信号(パルス列)の周波数分布を考える
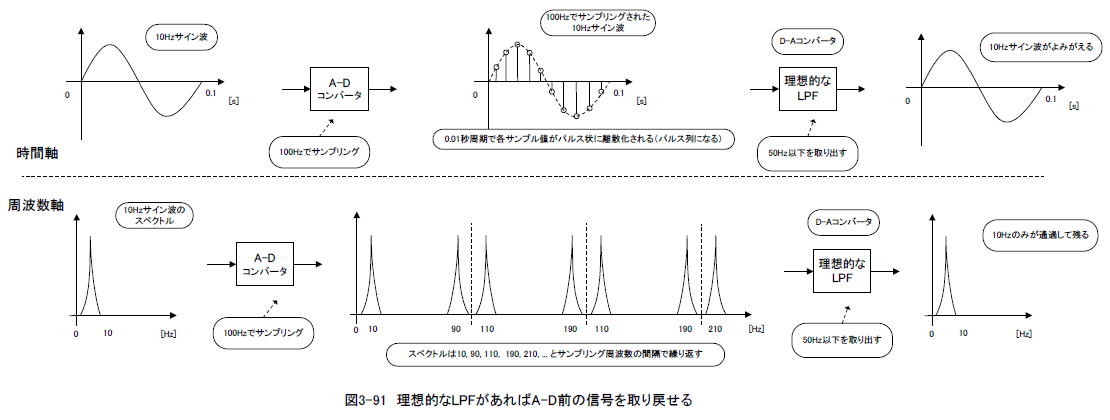
例えば「サンプリング周波数100Hzでサンプリングされた10Hzのサイン波」をフーリエ変換すると図3-91の下図(周波数軸)のように、スペクトルが10,
90, 110 , 190, 210 Hz ... と繰り返されます。このように離散化された信号(パルス列)の周波数分布は、サンプリング周波数の間隔で繰り返され、これは無限の周波数まで続きます。
言い換えると、「サンプリング周波数100Hzでサンプリングされた10Hzのサイン波」は 「10,
90, 110, 190, 210 Hz ... と繰り返されるサイン波を足し合わせたもの」と等価である、ということです。 |
■サンプリング周波数間隔で繰り返されるスペクトルを足し込んでいくスマホアプリ
それでは実際に「10, 90, 110, 190, 210 Hz ... と繰り返されるサイン波」を足し合わせるとどうなるでしょうか。図3-92のようにスマホアプリの「サンプリング定理の証明5」をタップしてみましょう。

●まずは10Hzと90Hzを足してみる
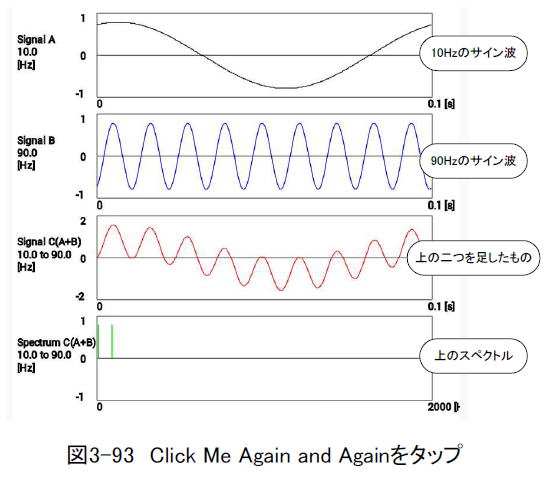
"Click me again and again"を1回クリックしましょう。(図3-93)一番上(Signal A)は10 Hz のサイン波です。二番目(Signal
B)は90 Hz のサイン波、三番目(Signal C)はSignal AとSignal Bを加算したものです。一番下(Spectrum
C)はSignal Cのスペクトルで、10 Hz と90 Hz に直線が二本立っています。
●10Hz + 90Hz + 110Hzはどうなるか
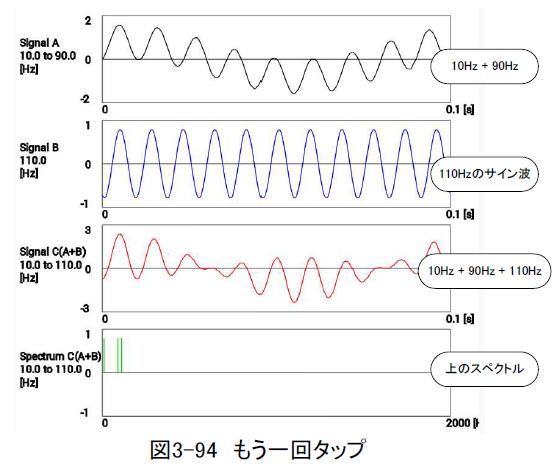
もう1回Click me again and againをクリックしてみましょう。(図3-94)するとSignal
Aは10 Hz と90 Hz を加算したものになり、Signal Bが110 Hz のサイン波になります。Signal
CはSignalA + Signal B、すなわち10 Hz , 90 Hz , 110 Hz が加算されたものになります(加算が進むごとにSignal
AとSignal Cの縦軸のスケールが増していきます)。Spectrum Cは10 Hz , 90 Hz
, 110 Hz に直線が立っています。
もう1回クリックするとSignal Cは10, 90, 110, 190 Hz を加算したものになり、少し波形が鋭くなってきましたね。(図3-95)

●390Hzまで足し込むとだいぶ鋭い波形になってくる
もう4回ほどクリックすると図3-96のようになります。10, 90, 110, 190, 210, 290, 310, 390 Hz のサイン波を足し合わせるとSignal Cはパルス列のように見えてきました。(縦軸のスケールを順次増やしています)

●890Hzまで足しこむとほぼパルス列の形になる
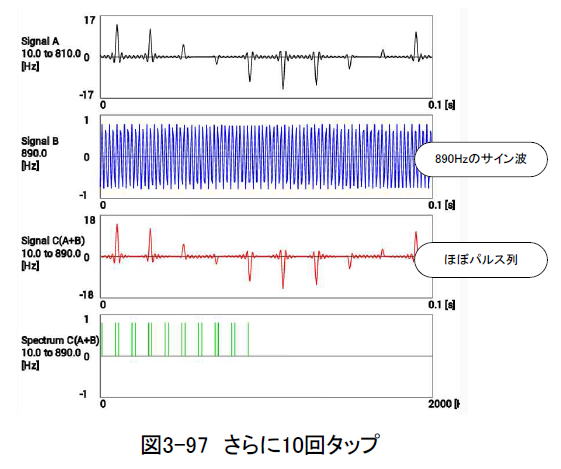
更に10回ほどクリックすると、Signal Cは10 Hz から890 Hz までの累積となり、その形状はほとんどパルス列になります。(図3-97)
●無限の周波数まで続けると「100Hzでサンプリングされた10Hz」と同じ形になる
このような累積加算を無限に続けるとSignal Cは完全なパルス列(パルスの幅がゼロ)となり、その包絡線は10 Hz のサイン波になります。(図3-98)
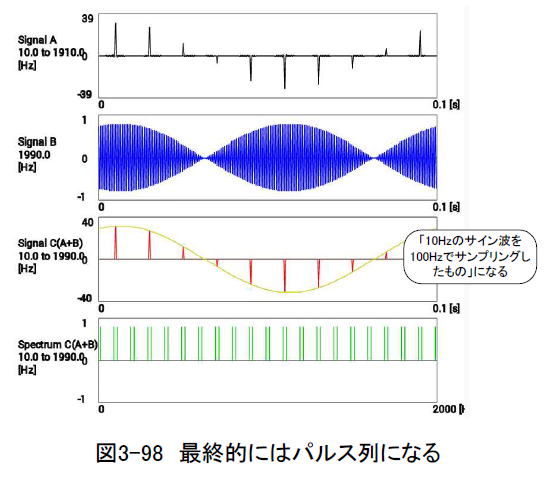
以上から、 「10 , 90, 110, 190, 210, Hz ... と繰り返されるサイン波を足し合わせたもの」と「サンプリング周波数100 Hz でサンプリングされた10 Hz のサイン波」は等価である、ということが分かります。
●40Hzでも同じ。サンプリング定理を守ればちゃんとよみがえる
スマホアプリのFreqボタンで周波数を40 Hz に変更して試してみましょう。結果は図3-99のようになり、包絡線は40 Hz のサイン波になります。
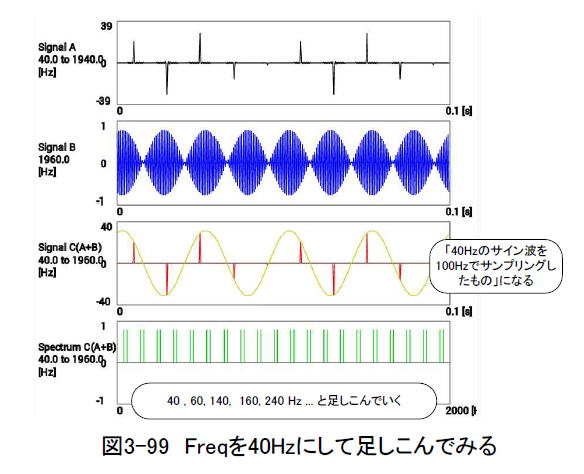
以上から、 「40 , 60, 140, 160, 240 Hz ... と繰り返されるサイン波を足し合わせたもの」と「サンプリング周波数100 Hz でサンプリングされた40 Hz のサイン波」は等価である、ということが分かります。
●原信号を復活させる条件
10Hz, 40Hzのサイン波で試しましたが、複数の周波数成分が混合した場合でも同様です。したがって図3-91のような、ナイキスト周波数(50Hz)以上を完全にカットする理想的なアナログLPFがあれば、原信号がよみがえることがわかります。
以上から更にもう一つ重要な定理を得ます。
サンプリング定理B: 原信号の最高周波数の2倍以上でサンプリングすれば、原信号を完全に復元することが可能である。
サンプリング定理というものは定理A(必要条件)と定理B(十分条件)の2つの定理からなります。どちらも大変重要な定理ですので、それらの意味を感覚的に理解してください。
本コラムではサンプリング定理について説明しましたが、それを厳密に証明するには複雑な数式に頼る必要があります。しかしそのように数式を羅列することは本企画の基本理念に反しますので、厳密な証明に関しては他著をご参考ください。
|
最初のページ
目次へ戻る
|

