A-01　アナログフィルタのEXCELシートの説明 　デジタルフィルタを設計する上ではアナログフィルタの知識も必要になります。このExcelをダウンロードして開いてみましょう。最初のREADMEシート（図A‐01）にEXCELファイルの簡単な説明があります。またアナログフィルタの係数は同図のように6個(A2, A1, A0, B2, B1, B0)になります（＊１） （＊１）デジタルフィルタの伝達関数はZ変換の式で表すのに対し、アナログフィルタはラプラス変換の式（同図のように"S"の関数）になります。 　　図A-01　最初のシートREADME ●隣のシートにアナログフィルタの係数がある 　f-responseシートを見ると図A‐02のようにD列にアナログフィルタの係数があります。上からA2, A1, A0, B2, B1, B0になります。これら係数に対する周波数特性をこのシートで計算します。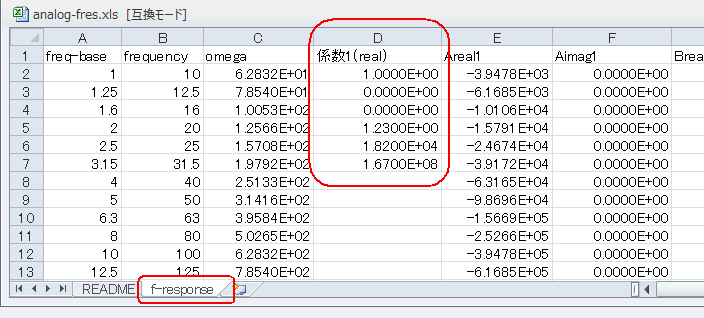 　　図A-02　周波数特性計算シート ●各周波数に対する特性を求める 　A列(freq-base)は1〜2000まで1/3オクターブの値です（＊２）。 　B列(frequency)はそれに定数（10、図A‐01のB4セル値）を掛けたもので、これらの周波数に対する周波数特性を求めます。 　C列(omega)はそれに（2π）を掛けたもので、角周波数になります。 （＊２）値が2倍になるまでに等比的に3ステップあるのが1/3オクターブ。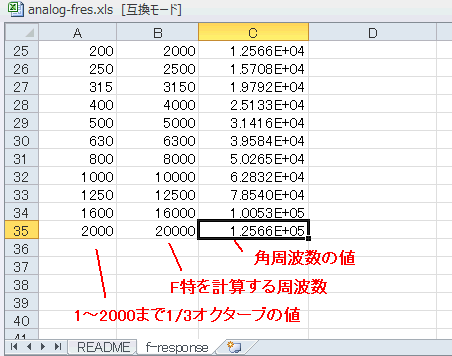 　　図A-03　この例では10〜20000HzまでのF特を求める ●周波数特性は複素数になる 　アナログフィルタの周波数特性の求め方はコラムA-02が参考になります。 　E列(Areal1)は同式の「分子の実数部」になります。またF列(AImag1)は同式の「分子の虚数部」になります。 　G列(Breal1)は同式の「分母の実数部」、そしてH列(BImag1)は同式の「分母の虚数部」です。 　図A‐04のように各セルをクリックするとEXCEL関数の式が表示されます。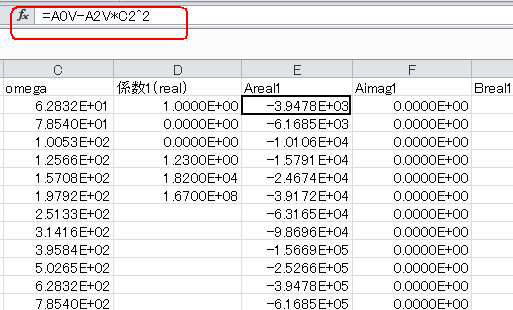 　　図A-04　各セルをクリックして計算法を見てみよう ●絶対値をdBでプロットする 　この式のH(ω）は複素数であり、その絶対値が振幅特性、角度が位相特性になります。図A-05の枠内の式のように対数をとってdB値とします（＊３）。 　frequency列を横軸、Gain[dB]列を縦軸としてプロットすると図A‐05のグラフになり、HPF（High Pass Filter, 高域通過フィルタ）であることが分かります。カットオフ周波数は約2kHzになります（＊４）。 （＊３）「分子の絶対値の2乗」を「分母の絶対値の2乗」で割る。2乗してあるので10*LOGで良い。 （＊４）正確には2055Hz。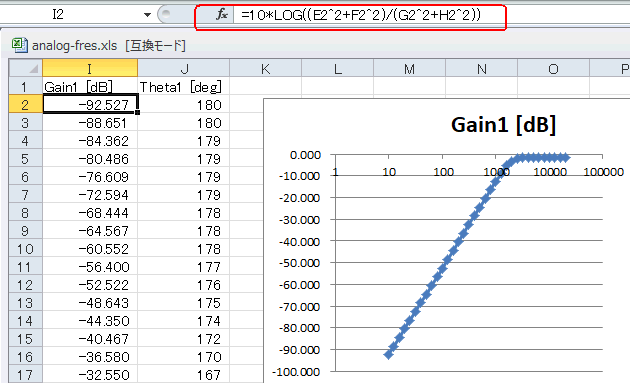ここで求めた係数を拝借 　　図A-05　HPFの特性。カットオフは約2kHz ●位相はATAN2関数で求める 　位相は図A-06のように求めます。（虚数部／実数部）のアークタンジェントで求まりますが（＊５）、EXCELでは"ATAN2"を使って角度を求めるのが良いでしょう（＊６）。 　frequency列を横軸、Theta[rad]列を縦軸としてプロットすると同図のグラフになります。HPFの場合はこのように進み位相特性になります。 （＊５） (AReal + j AImag) / (BReal + j BImag) = ((AReal + j AImag)(BReal - j BImag)) / ((BReal + j BImag)(BReal - j BImag)) 、分母が実数になるので、分子の実数部と虚数部で角度が決まる。前者がAReal*BReal + AImag*BImag、後者がAImag*BReal - AReal*BImagになる。 （＊６）"ATAN"関数は戻り値の範囲が-π/2〜+π/2であるのに対し、"ATAN2"関数は-π〜+πの範囲をとり得る。こちらの方が不連続点が少なくなってグラフが見やすくなる。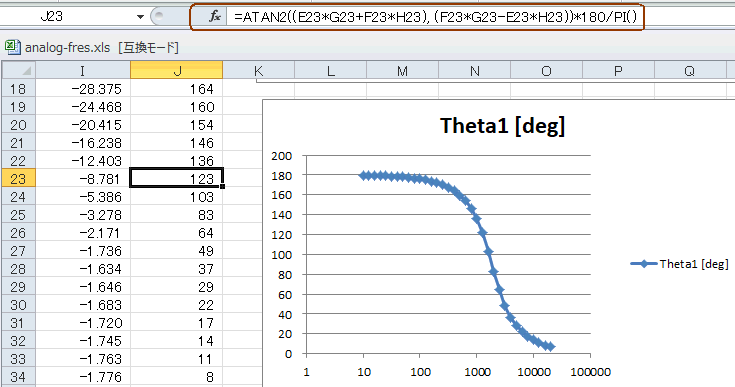 　　図A-06　低域では180度進む。単位はrad -> degreeとしている ●係数を変えてLPFにしてみる 　例えばこの係数をコピーしてD列にペーストすると図A-07のようなカットオフ約300HzのLPFになります。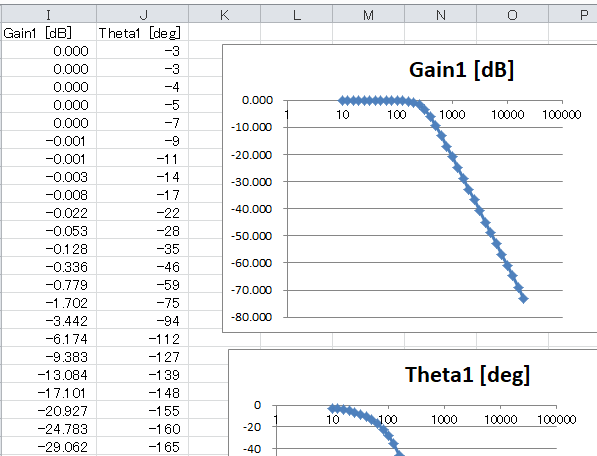 　　図A-07　LPFの特性。カットオフは約300Hz 目次へ戻る