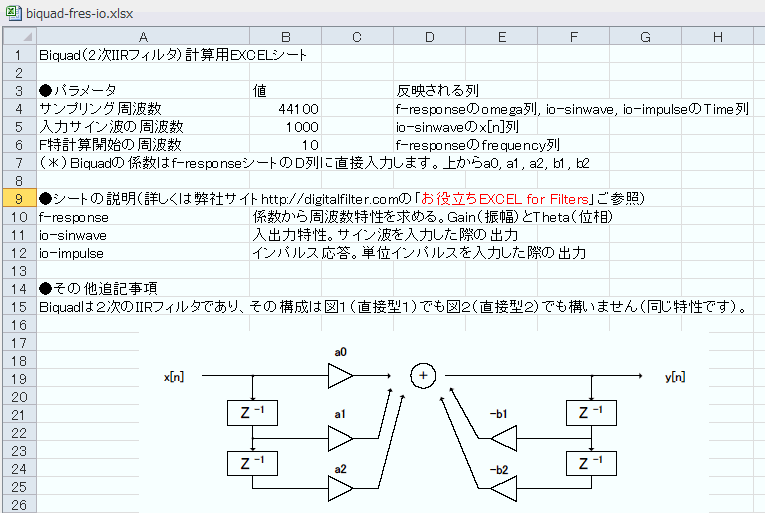
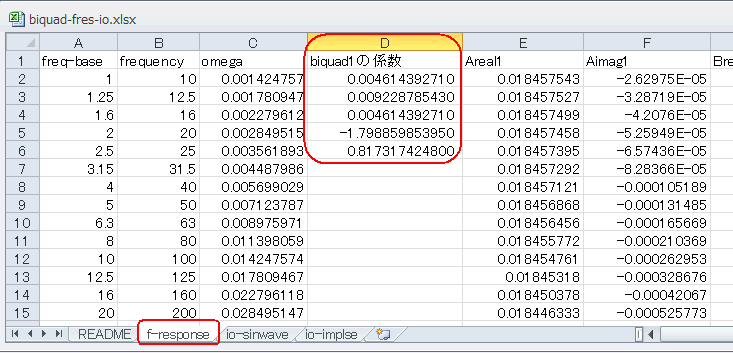
1-01　BiquadのEXCELシートの説明 　まずはIIRフィルタの代表格、Biquad（2次IIRフィルタ）です。このExcelをダウンロードして開いてみましょう。最初のREADMEシート（図1‐01）にEXCELファイルの簡単な説明があります。またBiquadの係数は同図のように5個(a0, a1, a2, b1, b2)になります（＊１） （＊１）フィードバック側の係数(b1, b2)は反転して足し込みます。 　　図1-01　最初のシートREADME ●隣のシートにIIRフィルタの係数がある 　f-responseシートを見ると図1‐02のようにD列にBiquadの係数があります。上からa0, a1, a2, b1, b2になります。これら係数に対する周波数特性をこのシートで計算します。 　　図1-02　周波数特性計算シート ●各周波数に対する特性を求める 　A列(freq-base)は1〜2000まで1/3オクターブの値です（＊２）。 　B列(frequency)はそれに定数（10、図1‐01のB6セル値）を掛けたもので、これらの周波数に対する周波数特性を求めます。 　C列(omega)はそれに（2π/サンプリング周波数）を掛けたもので、omega = πになる周波数がナイキスト周波数になります（＊３）。 （＊２）値が2倍になるまでに等比的に3ステップあるのが1/3オクターブ。 （＊３）この例ではサンプリング44100Hz（図1‐01のB4セル値）なので、ナイキストは22050Hz、その周波数でomegaがπ(=3.14)になる。20000Hzはナイキストの少し手前なので2.85[rad]になっている。 　　図1-03　この例では10〜20000Hzまで求める ●周波数特性は複素数になる 　Biquadの周波数特性はこのページの式2‐43で求まります。 　E列(Areal1)は同式の「分子の実数部」になります。またF列(AImag1)は同式の「分子の虚数部」になります。 　G列(Breal1)は同式の「分母の実数部」、そしてH列(BImag1)は同式の「分母の虚数部」です。 　図1‐04のように各セルをクリックするとEXCEL関数の式が表示されます。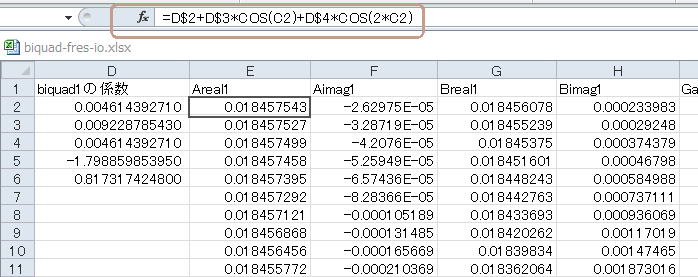 　　図1-04　各セルをクリックして計算法を見てみよう ●絶対値をdBでプロットする 　同式のH(ω）は複素数であり、その絶対値が振幅特性、角度が位相特性になります。図1-05の枠内の式のように対数をとってdB値とします（＊４）。 　frequency列を横軸、Gain[dB]列を縦軸としてプロットすると図1‐05のグラフになり、LPF（Low Pass Filter, 低域通過フィルタ）であることが分かります。カットオフ周波数（＊５）は1kHzになります。 （＊４）「分子の絶対値の2乗」を「分母の絶対値の2乗」で割る。2乗してあるので10*LOGで良い。 （＊５）減衰量が -3 [dB] になる周波数。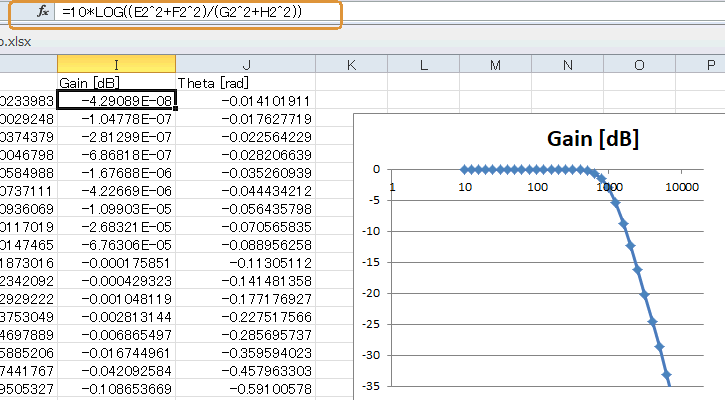 　　図1-05　LPFの特性。カットオフは1kHz ●位相はATAN2関数で求める 　位相は図1-06のように求めます。（虚数部／実数部）のアークタンジェントで求まりますが（＊６）、EXCELでは"ATAN2"を使って角度を求めるのが良いでしょう（＊７）。 　frequency列を横軸、Theta[rad]列を縦軸としてプロットすると同図のグラフになります。LPFの場合はこのように徐々に位相が遅れていきます。 （＊６） (AReal + j AImag) / (BReal + j BImag) = ((AReal + j AImag)(BReal - j BImag)) / ((BReal + j BImag)(BReal - j BImag)) 、分母が実数になるので、分子の実数部と虚数部で角度が決まる。前者がAReal*BReal + AImag*BImag、後者がAImag*BReal - AReal*BImagになる。 （＊７）"ATAN"関数は戻り値の範囲が-π/2〜+π/2であるのに対し、"ATAN2"関数は-π〜+πの範囲をとり得る。こちらの方が不連続点が少なくなってグラフが見やすくなる。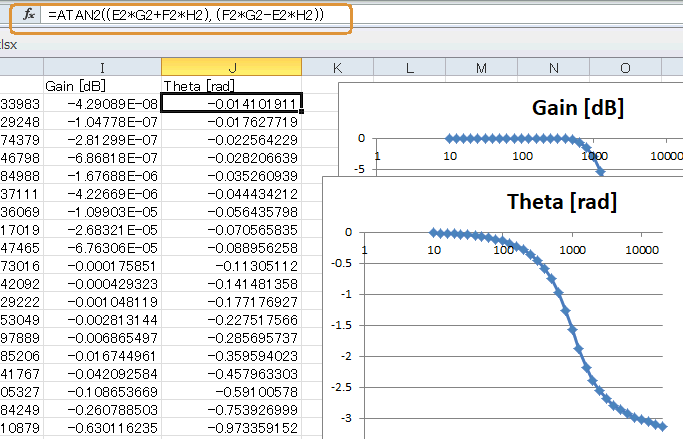 　　図1-06　位相は0〜πへと遅れていく 次のページへ 目次へ戻る