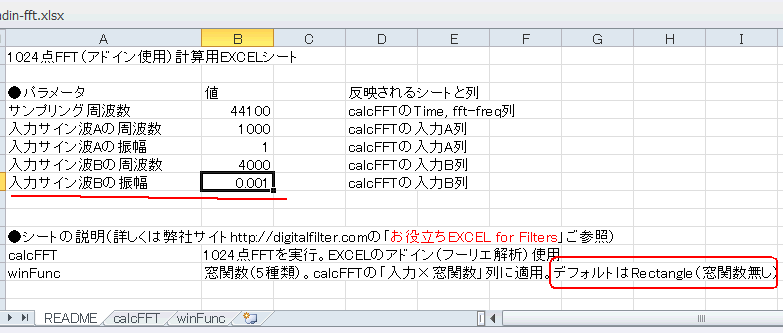
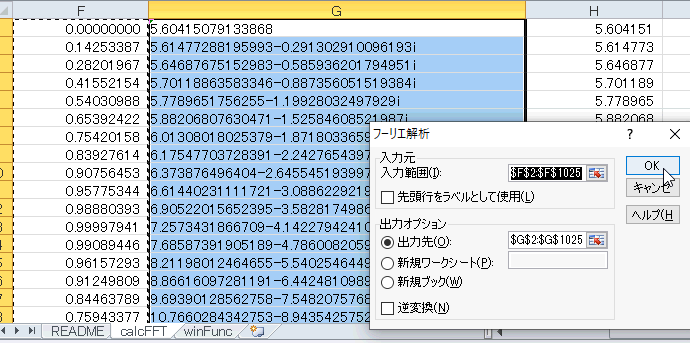
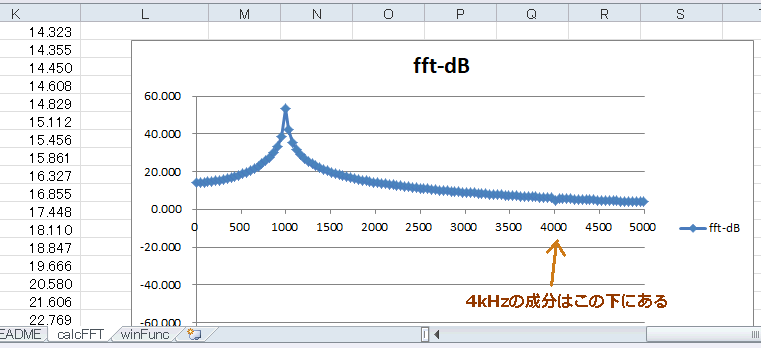
4-04　窓関数を使い分ける ●入力Bの振幅を小さくしてみる 　FFTで使用する「窓関数」はデフォルトではRectangle（窓関数無し）になっています（図4‐38）。この状態で入力Bの振幅を同図のように0.001とします。 　入力Aは1kHzで振幅1.0なのに対し、入力Bは4kHzで振幅0.001なので-60dBの微小成分になります。 　　図4-38　Bの振幅を0.001に（周波数は4000) 　入力を変更したら図4‐39のようにアドイン（フーリエ解析）を設定し直します（ここ参照）。 　　図4-39　アドインを設定しないと何も変わらない ●Rectangle窓はスペクトルのフロアが高い 　1kHzに対して4kHzの成分は-60dBなので、図4‐40のようにスペクトルのフロアに埋もれてしまっています。 　　図4-40　4000Hzにピークがあるはずが… ●入力×窓関数の列を変える 　それでは窓関数を変えてみましょう。F列の一番上を図4‐41のようにwinFuncを"F2"に変更し（＊１）、一番下まで引っ張ります。 （＊１）窓関数はwinFuncシートで生成。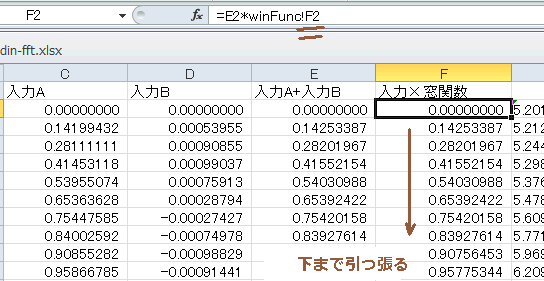図4‐41のようにするとBlackman-Harris窓が施される 　　図4-41　一番上だけ変更して後は引っ張るだけ ●Blackman-Harris窓なら微小成分も見える 　窓関数を変更したらアドイン（フーリエ解析）を設定し直します（ここ参照）。その結果は図4‐42のようになり、1kHzの他に4kHzも確認され、その振幅は-60dB低くなっています。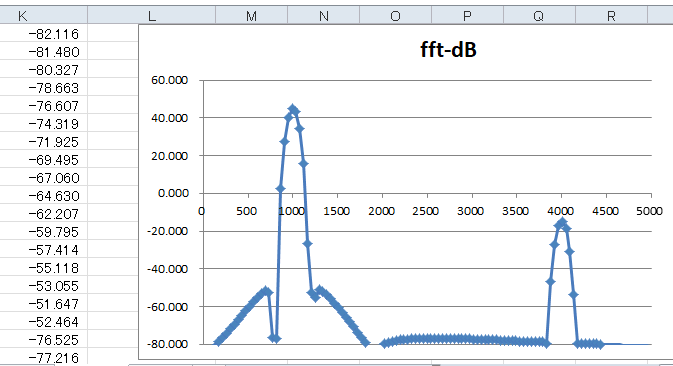 　　図4‐42　フロアが低いので4kHzが埋もれない ●Rectangleの弱点をBlackman-Harrisで克服 　窓関数はwinFuncシートで生成します。デフォルトではRectangle、図4‐43のように1024個すべて"1"になっており、入力にこれを乗算しても何も変わりません（すなわち窓関数無し）。このままFFTすると微小成分がスペクトルのフロアに埋もれてしまいます（図4‐40）。 　それに対しBlackman-Harrisは、微小成分も観測できるというメリットがあります（図4‐42）。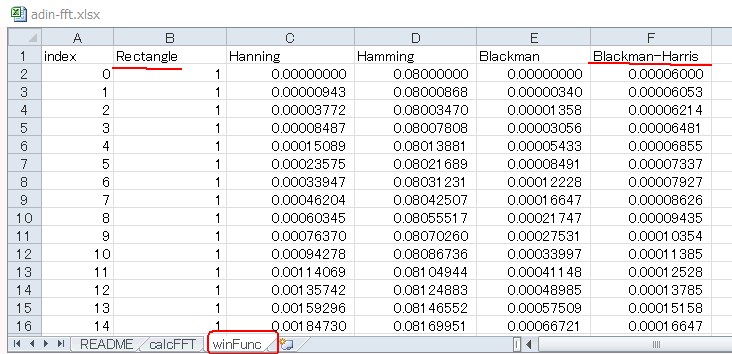 　　図4-43　winFuncシートを見る 　かといってRectangle窓はダメということではありません。次のページを見てみましょう。 次のページへ 目次へ戻る