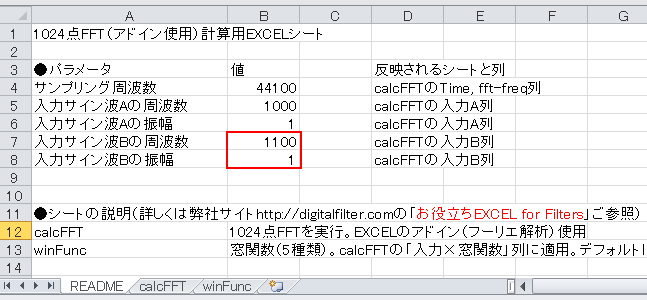
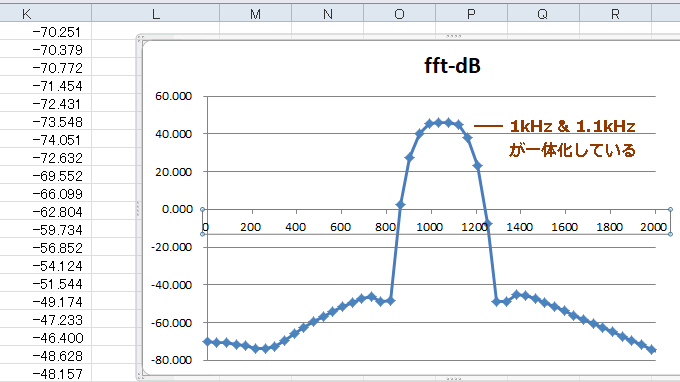
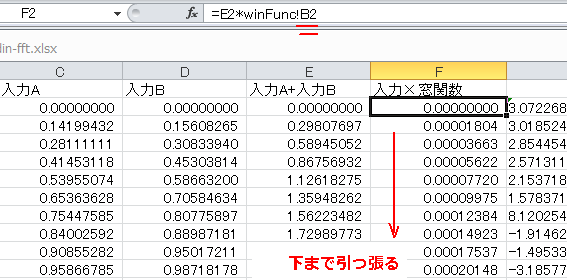
4-04　窓関数を使い分ける（続き） ●近接した周波数を足し合わせるとどうなるか 　Blackman-Harris窓には良い所ばかりではなく、弱点もあります。図4‐45のように入力Bの周波数を1100、振幅を1としてみましょう。入力AとBの周波数が非常に近いケースです。 　　図4-45　入力Bの周波数と振幅を変える ●1kHzと1.1kHzの区別がつかない 　入力を変更したらアドイン（フーリエ解析）を設定し直します（ここ参照）。その結果は図4‐46のように入力AとBのスペクトルが一体化しています。 　　図4-46　スペクトルが太いのがBlackman-Harrisの短所（横軸を拡大） ●入力×窓関数列を変更 　窓関数をRectangleに戻してみましょう。F列の一番上を図4‐47のようにwinFuncを"B2"に変更し、一番下まで引っ張ります。 　　図4-47　Rectangle窓ならどうなるか ●Rectangleなら近接した周波数が分かる 　窓関数を変更したらアドイン（フーリエ解析）を設定し直します（ここ参照）。その結果は図4‐48のようになり、1kHzの隣に1.1kHzも確認できます。 　このような入力に対してRectangle窓は有効、言い換えると「周波数分解能が高い」ということになります。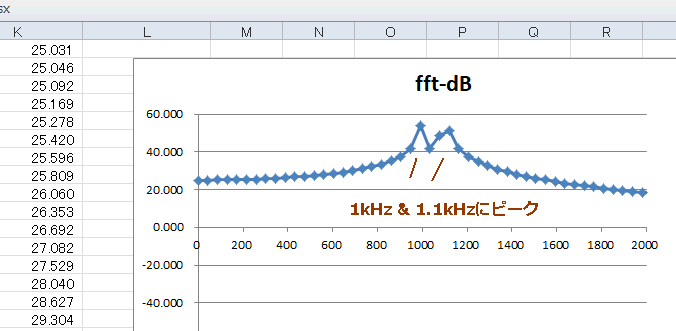 　　図4‐48　山が二つ見える！ ●振幅分解能と周波数分解能のトレードオフ 　まとめると表4‐01のようになります。このように窓関数には長所・短所があるので、状況によって使い分けましょう。良く分からないときはHanning窓がバランスがとれて良いかもしれません。 窓関数 振幅分解能 周波数分解能 Rectangle かなり低い かなり高い Hamming 低い 高い Hanning 普通 普通 Blackman 高い 低い Blackman-Harris かなり高い かなり低い 　　表4‐01　各窓関数のメリット・デメリット ●winFuncシートの右の方にグラフ 　各窓関数をグラフにすると図4‐49のようになります。各セルをクリックすると計算式が出てくるので参考にしてください。 　　図4‐49　各窓のグラフ（Rectangleは横一線になる） 最初のページへ 目次へ戻る