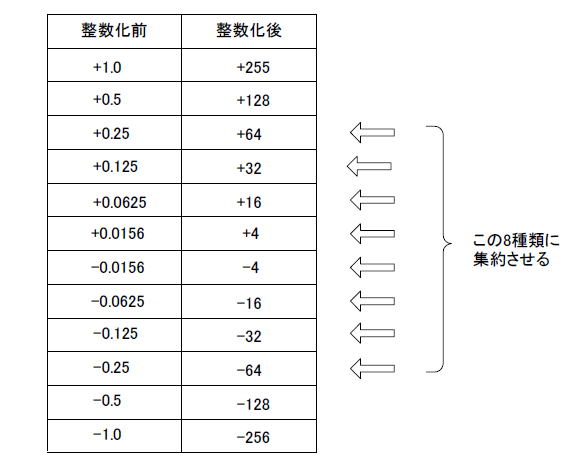
2-03 2層目は係数8種、ビットシフトで乗算器を節約 ●普通のFPGAには乗算器は100個もない 　1層目の係数は9x3x16 = 432個でしたが、2層目は9x16x32 = 4608個と多くなります。また3層目、4層目と進むにつれて更に係数の数は増えていきます。 　一つの層に必要な「乗算器の数」は「係数の数」に比例するので、普通に乗算するとFPGA内部の乗算器が足りなくなってしまいます（＊１） （＊１）このボード搭載のFPGA（5CSEMA5F31C6)には乗算器は87個しかない ●符号付9ビット整数化とは 　図2‐10は係数を整数化する際の対応です。「符号付き9ビット整数化」では、-1.0〜+1.0の範囲がこのように-256〜+255の範囲に写像されます。 図2‐10　-256〜+255の512段階だが… ●2の累乗ならビットシフト乗算ができる 　ハードウエアにおいて数値は2進数で扱われます。したがって図2‐10に示すような係数値（2の累乗）の場合、乗算は「ビットシフト」でまかなえます。 　例えば+64という係数をかけるなら、図2‐11のように6ビット左シフト、+16をかけるなら4ビット左シフトで済みます。-64や-16をかけるならなら符号を反転した後、同様にシフトさせます。このようにすれば乗算器を削減できそうです。 図2‐11　正の数ならシフトだけ、負の数なら符号反転してシフト ●閾値は-48, -24, -8, 0, 8, 24, 48で8種類に 　そこで思い切って、重み係数を８種類(+64, +32, +16, +4, -4, -16, -32, -64)に集約させます。Pythonでは図2‐12のように適当に閾値を設けて8種類に割り当てます。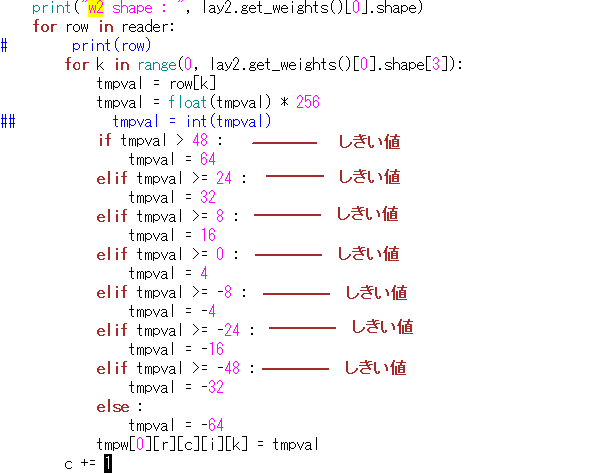 図2‐12　閾値によって値を割り振る ●2層目は「乗算器を使わない乗算」 　その結果、2層目の重み係数は図2‐13のように8種類にになります。すべて2の累乗なので「ビットシフトによる乗算」が可能になります。 　また、バイアスに関しては1層目と同じように普通に整数化します（加算なのでもともと乗算器は必要ない）。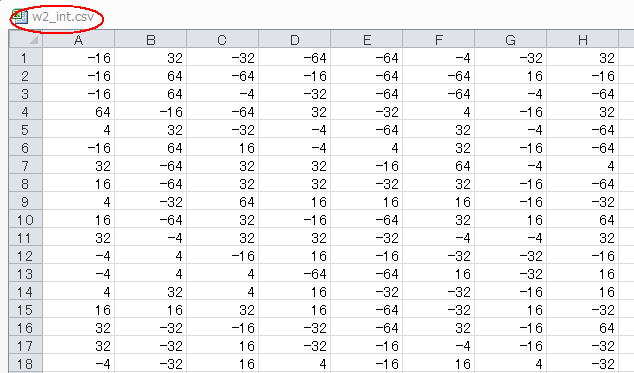 図2‐13　係数は+64, +32, +16, +4, -4, -16, -32, -64の8種類 次のページへ 目次へ戻る