7‐03 乗算器を使わないビットシフト乗算
●数万円台のボードのFPGAに乗算器はせいぜい100個
畳み込み2層目はこのように乗算器128個使って並列演算させますが、このボードのFPGAに乗算器は87個しかありません。したがってこのように「ビットシフトによる乗算」を行います。
ハードウエアにおいて数値は2進数で扱われます。したがって係数が2の累乗に限られる場合、乗算は「ビットシフト」でまかなえます。図7‐15にその一例を示します。 |
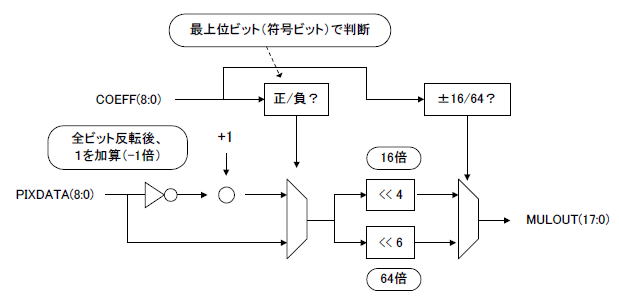
図7-15 ビットシフト乗算器の回路図
●乗算器の代わりになる回路
図7‐15は係数が4種類(+64, +16, -16, -64)に限られる場合です。画素データPIXDATAの全ビットが反転され、さらに1が加算されます。これは「-1倍」を意味します。
係数COEFFの最上位ビットは符号ビットで、0ならPIXDATA、1ならPIXDATA×(-1)がセレクタで選択されます。
セレクタの出力は4ビット、6ビット左シフトされ、16倍、64倍の値が生成されます。
最後にCOEFFの値が±16か±64かによってセレクタを切り替えます。これにより+64の場合は64倍、+16の場合は16倍、-16の場合は-16倍、-64の場合は-64倍の値が出力されMULOUTとなります(*1)。
(*1)2層目の係数はは8種類(+64, +32, +16, +4, -4, -16, -32, -64)なので、セレクタ入力がもう2つ(±4、±32)ある。
●1を足すだけならハーフアダーで済む
図7‐15には加算器(+1)がありますが、これは「ハーフアダー」というシンプルな回路でまかなえます(図7‐16)。 |
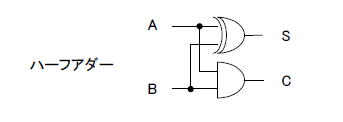 図7‐16 ANDとEXORだけ 図7‐16 ANDとEXORだけ
●9ビットなのでハーフアダーを9個縦続接続
ハーフアダーをビット数ぶん(9個)、図7‐17のように繋げば「+1」の回路の完成です。 |
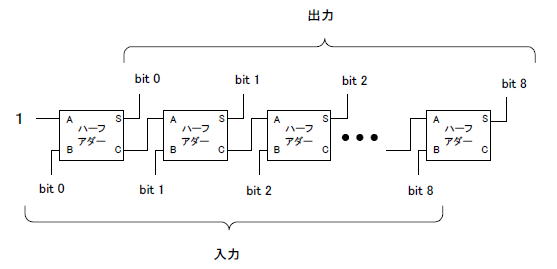
図7‐17 1を足すだけの9ビット加算器
●シンプルな回路なので128個あっても大丈夫
乗算器を128個も用意するのは現実的でないということで、「乗算器の代わりになる回路」を設計しました。このようにNOT,
AND, EXOR、シフタ、セレクタなど単純なロジックで構成されるため、128個あってもFPGAのリソースをそれほど圧迫しないでしょう。
●回路図をHDL化する
図7‐15では係数が4種類でしたが、2層目の係数はは8種類(+64, +32, +16, +4, -4, -16, -32, -64)なので図7‐18のようなHDLになります。
同図ではビットシフトは本来より2ビット少なくなっています(理由は図7‐19)。 |

図7‐18 VHDLで書いたビットシフト型乗算器
●本来の1/4になっているので・・・
2層目は入力16chを4chづつ4個の積和演算器で処理しますが(ここ参照)、それら4つを足し込む際(図7‐19のMacShift_XX)に2ビット左シフト(4倍)して相殺します。演算途中のビット数を減らしてFPGAのリソースを節約するためです。 |

図7‐19 dotproの外で4倍して相殺する
目次へ戻る
|

 図7‐16 ANDとEXORだけ
図7‐16 ANDとEXORだけ



 図7‐16 ANDとEXORだけ
図7‐16 ANDとEXORだけ

