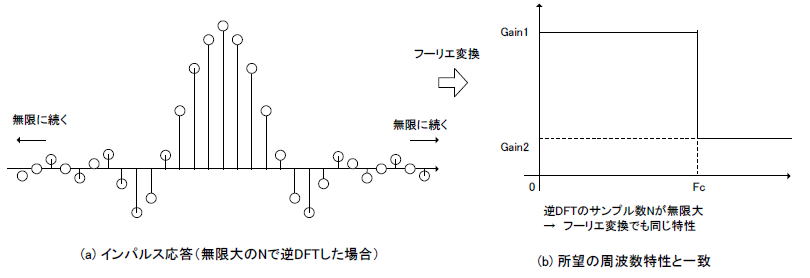
■窓関数を乗算してリプルを小さくする 図2-78(a)ではLPFの振幅特性を周波数0からFsまでN個サンプリングしていました。この際、例えばNの値が無限大、すなわちサンプル数が無限個であれば、その後の逆DFTによってインパルス応答は図2-82(a)のようになり、無限に続きます。このインパルス応答をフーリエ変換(DFTではない!)すると周波数特性は同図(b)のように所望の周波数特性と同一になります。
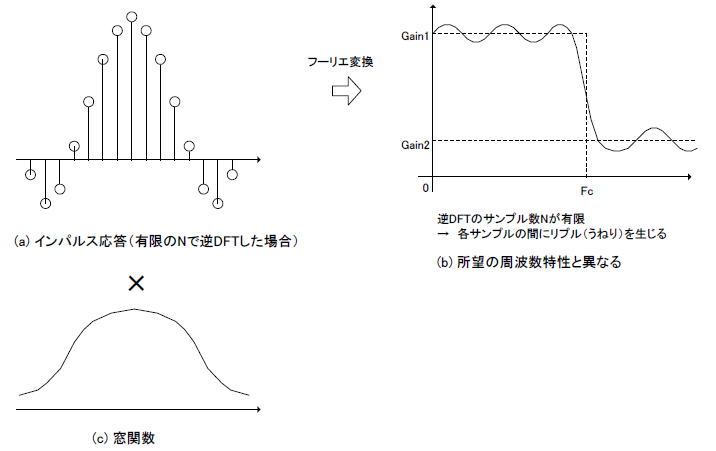
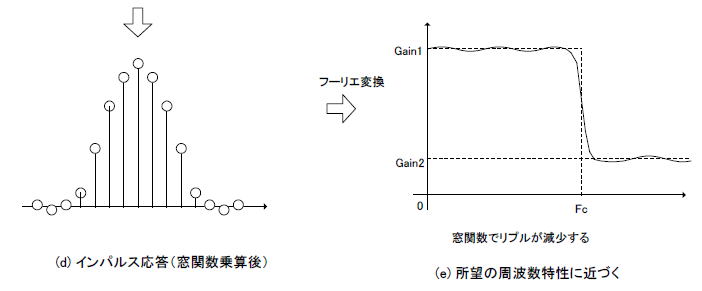
●係数の数を制限すると特性が波打つ しかしNが無限大の場合はタップ数(フィルタ長)が無限大になってしまい実現不可能なので、Nは有限の値にならざるを得ません。その場合、インパルス応答も図2-83(a)のように有限長(N個)で打ち切られた形になります。このインパルス応答をフーリエ変換すると周波数特性は同図(b)のように通過域、阻止域にリプル(ripple、小さく波打つ、さざ波)を生じます。これは逆DFTする前段階、所望の振幅特性を離散化する際、Nが小さいため各サンプルの間が開きすぎたことによります。 ●窓関数でリプルを低減する このようにNの数が少ないほど所望の周波数特性から離れていきますが、それを低減するためには「窓関数」が有効です。図2-83(c)はその一例で、これと同図(a)のインパルス応答(有限長)と掛け合わせると同図(d)のようになります。 それをフーリエ変換すると同図(e)のように通過域、阻止域のリプルが減少します。
●カイザー窓で係数の始まりと終わりの値を小さめにする ここで窓関数の一種、「カイザー窓」について説明します。それは次式で与えられます。 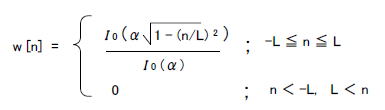 式2-25 カイザー窓の定義 式2-25 カイザー窓の定義Lは窓関数の幅を決めるパラメータで、タップ数(フィルタ長)をNとすると、N=2L+1の関係があります。αは窓関数の形状を決定するパラメータで、いくつかのαにおいて描画すると図2-84のようになります。 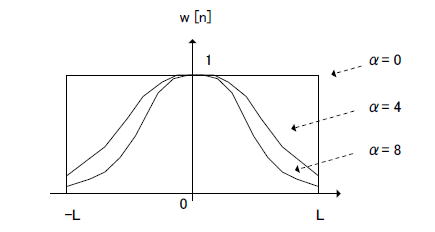 図2-84 いくつかのαにおけるカイザー窓 またαを増大すると阻止域のサイドローブが減少します(図2-85)。また、Io(x)は0次第1種変形ベッセル関数です。これに関しての詳しい説明は省略しますが、興味のある方はラズベリーパイ用のCソースコード(コラム27で使用)を参照してください。 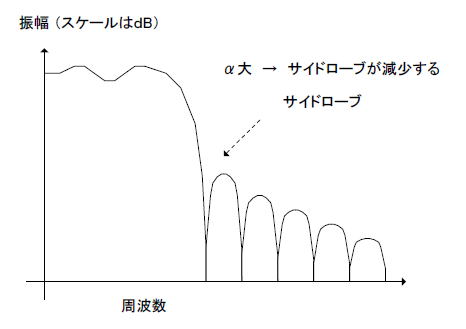 図2-85 αと阻止域サイドローブの関係 ●「窓関数法」によるFIRフィルタ係数の導出 カイザー窓はこのように自由度が高いためFIRフィルタの設計によく使われます。FIRフィルタの設計手順(窓関数法という)をまとめると次のようになります。 ①設計仕様の決定(通過/減衰域、通過/減衰量、タップ数など) ②振幅特性の離散化 ③逆DFT ④インパルス応答のシフト ⑤窓関数の乗算 ●コラム27ではラズベリーパイを使ってFIR係数を導出します。 最初のページへ 目次へ戻る |