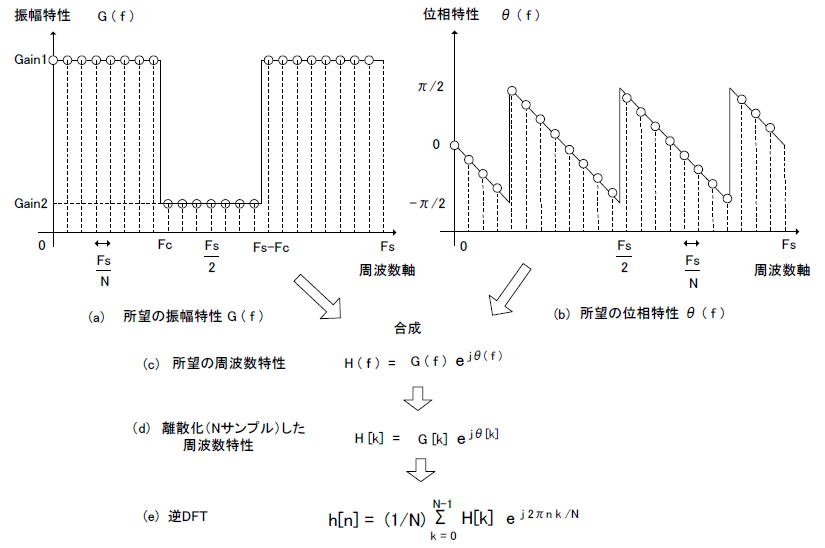
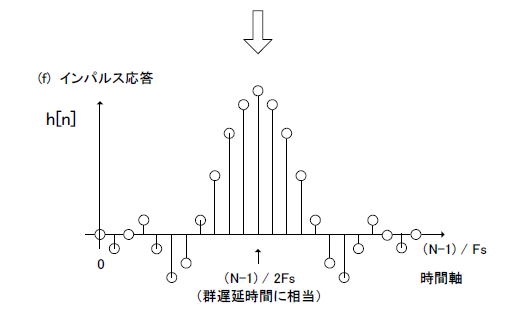
| コラム26 FIRフィルタの係数を求める方法 ●周波数特性を逆DFTするとインパルス応答(FIR係数)が求まる コラム25で述べたように、インパルス応答のDFTはそのシステムの周波数特性となります。 ということは、逆に周波数特性を逆DFTするとインパルス応答が得られます。FIRフィルタの場合、インパルス応答がその「係数」に等しくなるため、逆DFTを使用した係数導出法がよく用いられます。 係数と周波数特性の関係をまとめるとこのようになります。 インパルス応答(FIR係数) −−−−−→ 周波数特性 DFT(式2-20) 周波数特性 −−−−−→ インパルス応答(FIR係数) 逆DFT(式2-21) ■手順1:所望の振幅特性と位相特性を与える係数導出法 それでは周波数特性からインパルス応答(FIRフィルタの係数)を導き出す手順を説明します。 ●周波数に対して振幅がどのような特性をとるか決める まず所望の振幅特性G(f)を決定します。例えばLPFを設計したい場合図2-77(a)に示すような振幅特性を考えます。カットオフ周波数FcまではGain1という大きいゲインを与え、Fcを超える周波数ではGain2という小さいゲインを与えます。また離散信号ゆえに振幅特性はナイキスト周波数(サンプリング周波数の半分、Fs/2)を軸に対称になるので、Fs/2〜Fs-FcまではGain2、Fs-Fc〜FsまではGain1というゲインを与えます。 ●周波数に対して位相は直線的に遅れていく 次に所望の位相特性θ(f)を決定します。これから設計するFIRフィルタは「直線位相特性」(コラム26で解説)と仮定すると、位相特性は図2-77(b)に示すように直線的なギザギザ波形になります。(*1) (*1)ギザギザ(不連続点)があるのは位相特性の定義式(式2-14)にアークタンジェントが含まれるためで、感覚的にはまっすぐ斜め下に向かって伸びていると考える。 ●振幅特性に位相特性を掛け合わせる 振幅特性G(f)と位相特性θ(f)を合成して図2-77(c)のように「所望の周波数特性H(f)」となります。 ●周波数特性を離散化させて逆DFTすれば係数が求まる それから周波数特性を離散化します。周波数軸の0からFs(サンプリング周波数)までをN等分して離散化します。(図2-77(d)) 最後に逆DFTを行います(同図(e))。その結果インパルス応答h[n](同図(f))が求められます。FIR型フィルタなのでインパルス応答の形がそのまま「係数」になります。
●群遅延時間はインパルス応答の中心 また直線位相特性なので、群遅延時間は(N-1)/2Fs になり、その位置はインパルス応答の中心になります。(コラム26で解説) ●実際の係数導出法 これでFIRフィルタの係数導出は終了ですが、実際的にはこのような「所望の位相特性を与える手法」はあまり使用されません。「次のページへ」をクリックしましょう。 次のページへ 目次へ戻る |