コラム25　インパルス応答をDFTして周波数特性を求めることもできる 　コラム24では図2-73に示すステップで周波数特性を求めていました。しかしここではZ変換を介さず、DFTにより求める方法を説明します。 　図2-73　コラム24ではこの方法を使った 　インパルス応答h[n], n = 0, 1, 2, ... N-1をZ変換すると、 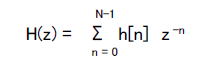　ここでとおくと、周波数特性が得られます。 　上式の角周波数ωを式1-5の右辺で置き換えると次のようになります。 ここで　k = 0, 1, 2, .... N-1　式2-20 ●インパルス応答→周波数特性はDFTを使ってもできる 　上式をよく見るとDFTの定義式（式1-3）と同じです。すなわち、インパルス応答をDFTすると、そのデジタルフィルタの周波数特性になるということです。DFTの結果（スペクトル）は、その周波数特性を等間隔(Fs/N、Fsはサンプリング周波数、Nはインパルス応答の数)でサンプリングした値に対応します（図2-74）。 　図2-74　インパルス応答のDFTは周波数特性を離散化したものに等しい ●周波数特性→インパルス応答は逆DFTを使えばよい 　逆に周波数特性が分かればそれを「逆DFT」（式1-4）することによりインパルス応答を求めることができます。FIRフィルタの係数はインパルス応答に等しいため、その設計に逆DFTがよく用いられます。 　式1-4のx[n]をh[n]に変更したものを次に示します。 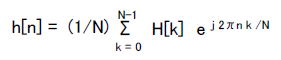ここで　n = 0, 1, 2, .... N-1　式2-21 ●コラム26にFIR係数の導出方法、コラム27でその実習をします。 目次へ戻る