コラム24　伝達関数から周波数特性を求める手順 　ここでは「7サンプル移動平均フィルタ」（＊１）の周波数特性を求めます。 （＊１）一種のFIRフィルタです。IIRフィルタの周波数特性はコラム2Bで。 ●インパルス応答→伝達関数 　漫画23で述べたように、7サンプル移動平均のインパルス応答は次のようになります。 h[n] = { h[0] = 1/7, h[1] = 1/7, h[2] = 1/7, h[3] = 1/7, h[4] = 1/7 , h[5] = 1/7 , h[6] = 1/7 } 　これをZ変換（式2-6）すると次のように伝達関数が求まります。 ●伝達関数→周波数特性 　伝達関数から周波数特性を求めるにはH(z)において次のように変数変換します。Tはサンプリング周期、ωは角周波数、jは虚数単位です。 　なおここでは簡単のため、次のようにT=1と正規化（サンプリング周期1s、サンプリング周波数1Hz）します。 　その結果、7サンプル移動平均の伝達関数H(z)は角周波数の関数H(ω)になります。 　式2-10 ●オイラーの公式を使って実数部と虚数部に分ける 　ここで次のオイラーの公式を適用します。 　上式において x = -nωとおくと次のようになります。 　これを式2-10に代入すると7サンプル移動平均の周波数特性は次のようになります。 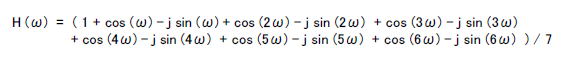　ここでH(ω)を実数部HReal(ω)と虚数部HImag(ω)に分けると次のようになります。 　すると実数部は次のようになります。 式2-11 　また虚数部は次のようになります。 式2-12 ●複素ベクトルの絶対値と角度に分ける 　このように周波数特性が複素数で表されているので、複素ベクトルの絶対値G(ω)と角度θ(ω)に分けることができます。 　ここでG(ω)は「振幅特性」、θ(ω)は「位相特性」と呼ばれ次の式2-11、式2-12で求められます。 　式2-13 　式2-14 　式2-11、式2-12を式2-13に代入すると7サンプル移動平均の振幅特性は次のようになります。 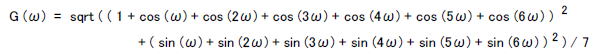式2-15 また式2-11、式2-12を式2-14に代入すると7サンプル移動平均の位相特性は次のようになります。 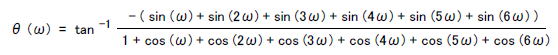式2-16 ●計算機を使って計算、振幅はデシベルで表す 　振幅特性（式2-15）と位相特性（式2-16）は複雑な計算を伴うため、通常は計算機を用いて計算します。その結果は図2-68のようになります。横軸は「角周波数」です。Gainが振幅特性、Phaseは位相特性で、Gainの単位はデシベル、Phaseの単位はラジアンです。 　振幅、位相特性ともにω=2πの間隔で繰り返す周期関数になります。したがって0 ≦ ω < 2πの期間で評価すれば十分です。また、一般的に振幅特性G(ω)は対数グラフで表示されるほうが見やすいため、次のようにに基数が10の対数をとり２０倍した後、単位をデシベル[dB]で表します。 　図2-68　7サンプル移動平均の正規化角周波数特性 ●サンプリング周波数 1Hz での周波数特性が求まる 　図2-68の横軸は「角周波数」ですが、それを「周波数」にするにはスケールを2πで除算します（図2-69）。右端がサンプリング周波数に相当し、1Hz になります。また真ん中は0.5Hz ですが、このような（サンプリング周波数／２）の周波数を「ナイキスト周波数」と呼びます。 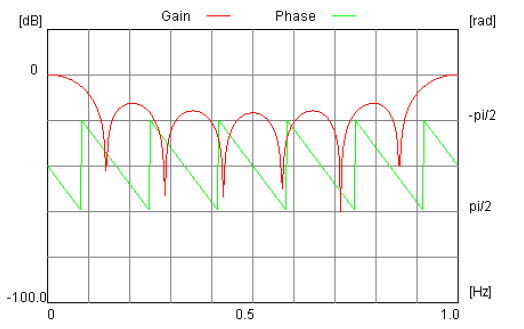　図2-69　7サンプル移動平均の正規化周波数特性（サンプリング周波数 = 1Hz） ●横軸のスケールにサンプリング周波数を乗算すればよい 　図2-69はサンプリング周波数 1Hz での周波数特性（これを「正規化された周波数特性」という）ですが、実際の回路は様々な速度で使用するので、任意のサンプリング周波数に対する周波数特性を求めなければなりません。 　仮に7サンプル移動平均フィルタをサンプリング周波数 22050Hz で動作させるとき、その場合は横軸のスケールにそのサンプリング周波数を乗算します。サンプリング周波数が変わっても特性の形（サンプリング周波数に対する、カットオフ周波数などの位置関係）は変わりません。（図2-70）。すなわち横軸のスケールのみを変更すると考えてください。 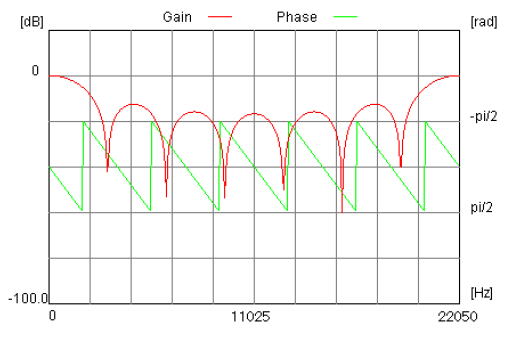　図2-70　7サンプル移動平均の周波数特性（サンプリング周波数 = 22050Hz） ●周波数特性を求めるプログラム 　図2-71は周波数特性を計算・描画するプログラムfirfres.c （コラム23で使用）の一部です。このように「正規化角周波数特性」を求め、描画する際、横軸をサンプリング周波数に合わせます。 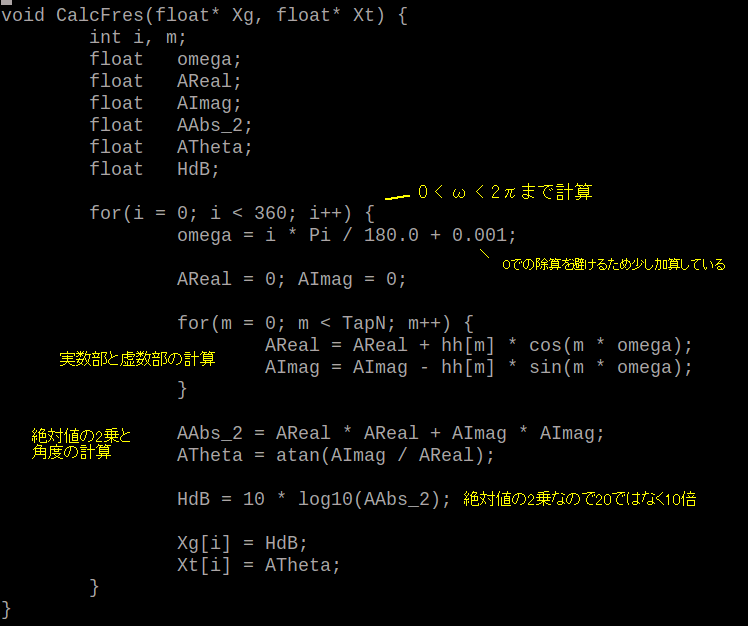　図2-71　周波数特性を計算するC言語ソースコード(firfres.c)の一部 目次へ戻る