■双一次S-Z変換 　双一次S-Z変換によってアナログフィルタをデジタルフィルタに変換します。次に変換公式を示します。 　双一次S-Z変換によりH(s)はH(z)に変換されますが、変換前のアナログ周波数特性H(Ω)と変換後のデジタル周波数特性H(ω)の関係は線形ではなく非線形な関係になります。 ●あらかじめプリワーピングでカットオフ周波数をずらした理由 　アナログの周波数特性は図2-153のように無限の周波数まで続くのに対し、デジタルの周波数特性はナイキスト周波数で終わります。したがって双一次S-Z変換を行うと高域のアナログ周波数特性をぐっと圧縮してデジタル化する格好になり、それに伴いカットオフ周波数には「ずれ」が生じます。これを避けるために、式2-52のようなプリワーピングを行い、あらかじめカットオフ周波数をずらしておくわけです。 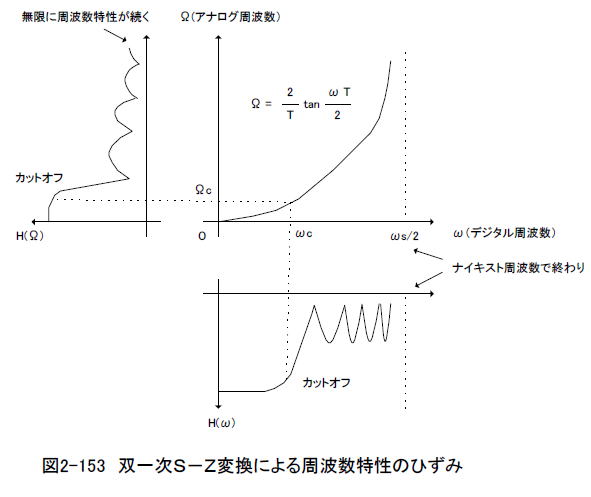●実際に双一次S-Z変換してみる 　さて、式2-57の双一次S-Z変換公式を代表的な1次式、2次式に施して整理したものを表2-13に示します。 　　　　表2-13　1次式、2次式のＳ−Ｚ変換法 （＊２） 　式2-56のアナログHPFを表2-13にのっとって次のようにパラメータを計算します。 α = 2 x 22050 = 44100 β = 1 x 44100^2 = 1.94 x 10^9 G = 1 / (44100^2 + 1.82 x 10^4 x 44100 + 1.67 x 10^8) = 3.43 x 10^-10 A = 1.82 x 10^4 B = 1.67 x 10^8 C = 1 D = E = 0 　以上のようにパラメータが求まり、表2-13の右下の式に当てはめると次のようになります。 β + Dα + E = 1.94 x 10^9 + 0 + 0 = 1.94 x 10^9 2(E - β) = 0 - 2 x 1.94 x 10^9 = -3.88 x 10^9 β - Dα + E = 1.94 x 10^9 - 0 + 0 = 1.94 x 10^9 2G(B - α^2) = 2 x 3.43 x 10^(-10) x (1.67 x 10^8 - 44100^2) = -1.22 G(α^2 - Aα + B) = 3.43 x 10^(-10) x (44100^2 - 1.82 x 10^4 x 44100 + 1.67 x 10^8) = 0.449 　すると次のようなZ変換の式になります。 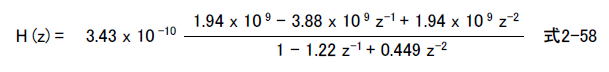　さらに整理すると双一次S-Z変換の結果は次のようになります。 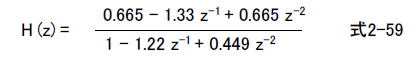●カットオフ周波数2000HzのデジタルHPFの出来上がり！ 　式2-59は2次IIRフィルタ（Biquad）です。この係数で周波数特性を計算すると、図2-154のようにカットオフ周波数2000HzのHPFになっています（ラズベリーパイで計算・描画）。 ●ラズベリーパイで計算してみよう 　コラム2FではIIRフィルタの係数を導出するプログラムをラズベリーパイで走らせます（バタワース型のLPF/HPF/BPF/BRF)。 （＊２）参考文献 以下の文献から引用。 「ディジタル・フィルタ設計入門」、尾知博、CQ出版社、1990年 「実践ディジタル・フィルタ設計入門」、岩田利王、CQ出版社、2004年 最初のページへ 目次へ戻る