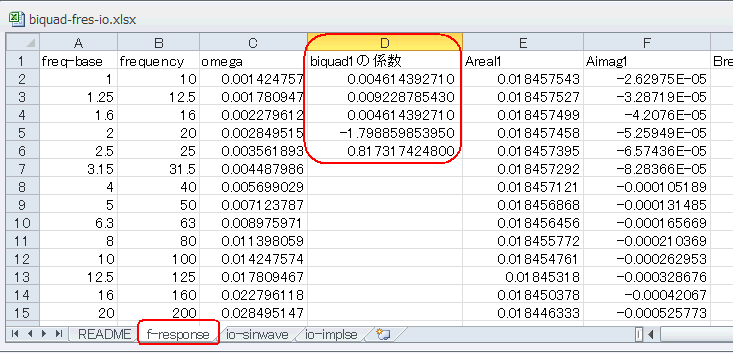
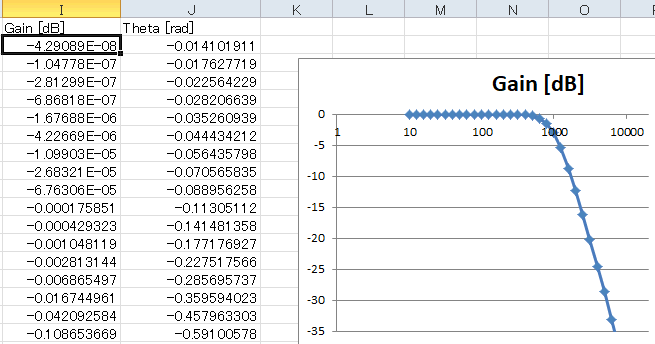
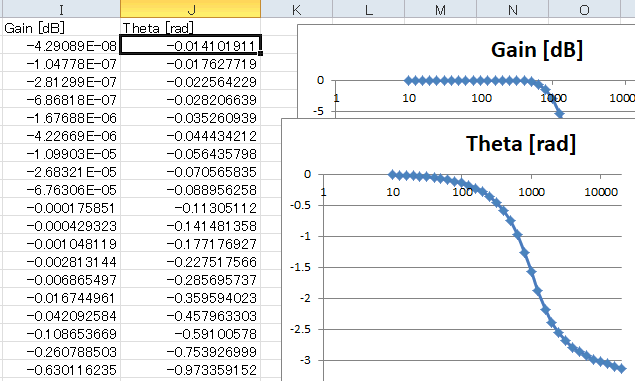
コラム35　EXCELでIIRフィルタを実行する 　ここで使用したEXCELのf-responseシートを開きます。下図のようにD列にBiquadの係数があります。上からa0, a1, a2, b1, b2になります。これら係数に対する周波数特性をこのシートで計算します。 　　　　　　f-responseシート 　このシートの右の方に振幅特性があります（下図、求め方はここ）。LPF（Low Pass Filter, 低域通過フィルタ）であることが分かります。カットオフ周波数は1kHzになります。 　　　　　　　　　　　　　LPFの特性。カットオフは1kHz 　振幅特性の下に位相特性があります（下図、求め方はここ）。LPFの場合はこのように徐々に位相が遅れていくのが分かります。 　　　　　　　　　　　　　位相は0〜πへと遅れていく ●サイン波の入出力を計算するシート 　隣のシートio-sinwaveを見てみましょう。A列(index)に0〜2047、B列(Time)はそれをサンプリング周波数（44100、READMEのB4セル)で割ったものです。C列(x[n])は下図の式で示すようなサイン波になります（＊１） （＊１）この例では1kHz（READMEのB5セルが1000）のサイン波になる。すなわち44100/1000サンプルで一回転（2π）する。 　D列は係数ですが、これらはf-responseシートのD列から転写されます。したがってもし係数を変える際はこのシートではなくf-responseシートの方を変更してください。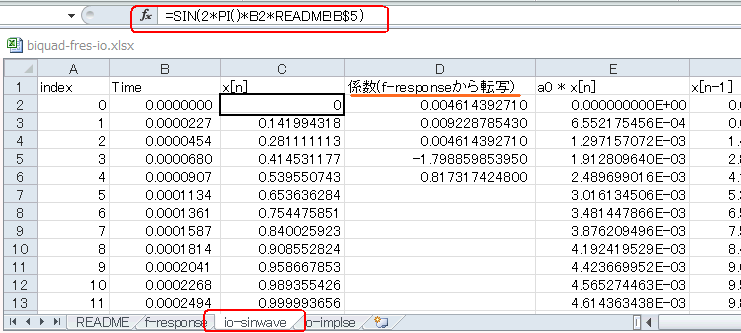 　　　　　　隣のシートを見てみる ●フィルタ演算は遅延→乗算→累積 　E列以降はこのブロック図のような演算を行います。E列は入力x[n]に係数a0を乗算します（下図）。そしてF列x[n-1]は、x[n]を１サンプル遅延したものです。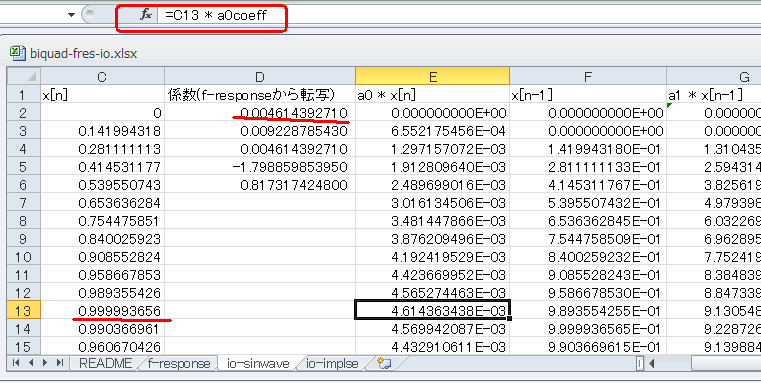 　　　　　　　C列にD2セルを乗算したものがE列 ●a0, a1, a2を各列に掛ける 　F列にa1を掛けたものがG列になります（下図）。F列をさらに１サンプル遅延させたものがH列、それにa2を掛けたものがI列になります。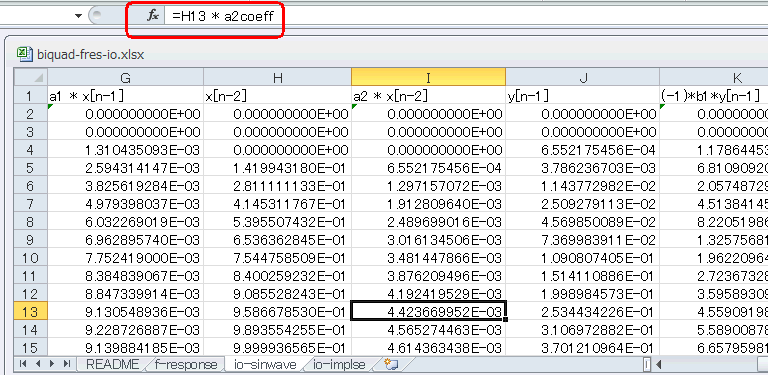 　　　　　　このブロック図を実践している ●b1, b2は反転して乗算 　J列以降はこのブロック図のフィードバック側の計算です。N列がBiquadの出力y[n]、それを1サンプル遅延したものがJ列y[n-1]、それを2サンプル遅延したものがL列y[n-2]になります（＊２）。 　それらに係数をかけたものがK、M列ですが、下図のように符号を反転させていることに注意しましょう（＊３）。 （＊２）遅延器の初期値はすべて０になっています。 （＊３）フィードバック側係数の符号に関してはここ参照。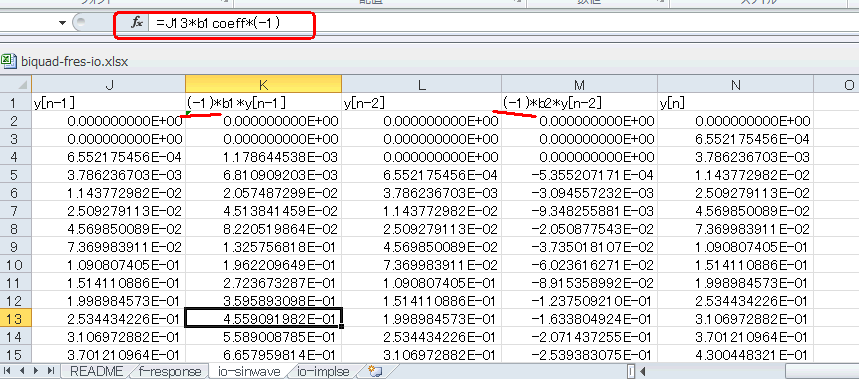 　　　　　　　このブロック図と合っているか確認 次のページへ 目次へ戻る