4-03 1024点FFTを実行しよう!
●実際のFFTは1024点以上ある
FFTは点数が多いほど精度が上がり、1024点にもなるとかなり精密な周波数解析ができます。このEXCELをダウンロードして開いてみましょう。最初のREADMEシート(図4‐30)にEXCELファイルの簡単な説明があります。
FFTはEXCELのアドイン(フーリエ解析)を使用したもので、点数は1024固定、サンプリング周波数や入力信号はこのシートで変更します。 |
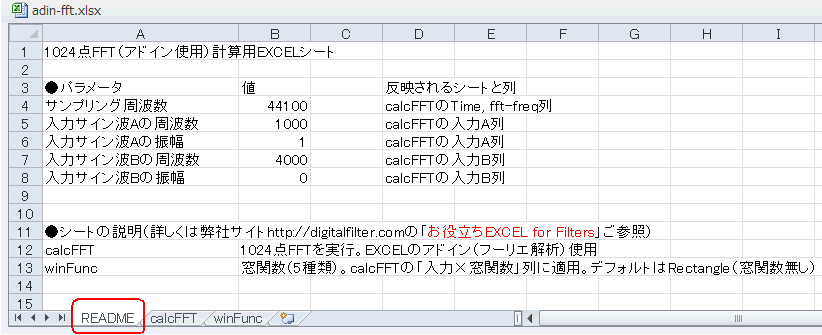
図4-30 最初のシートREADME
●calcFFTシートでサイン波生成
READMEシートでは入力サイン波Aは1000Hzで振幅が1、入力サイン波Bは4000Hzで振幅が0になっています。A+BがFFTの入力となりますがBの振幅がないので、図4‐31(calcFFTシート)のように実質的に1000Hzのサイン波をFFTすることになります。 |
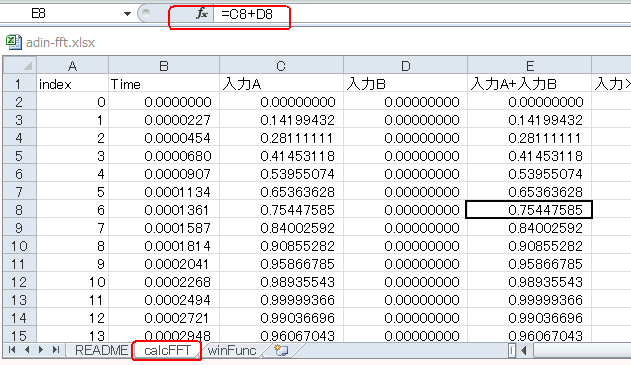
図4-31 calcFFTシートを見る
●窓関数を施してからFFT
その隣のF列では「窓関数」を乗算しますが、デフォルトでは窓関数はなし(*1)になります。したがって図4‐32のようにE列がそのままF列となります。
(*1)窓関数はwinFuncシートで生成。デフォルトではRectangle窓(窓関数無し)を使用。詳しくは次章で説明する。 |
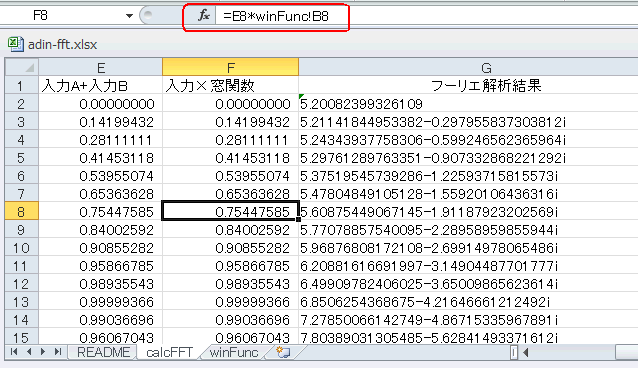
図4-32 セルをクリックすると計算式
●FFT結果は実数部と虚数部からなる
F列をFFTしたものがG列になります。EXCELのアドイン(フーリエ解析)を使用しています(ここ参照)。その結果は複素数になり、その隣のH列/I列で実数部/虚数部を分離しています。 |
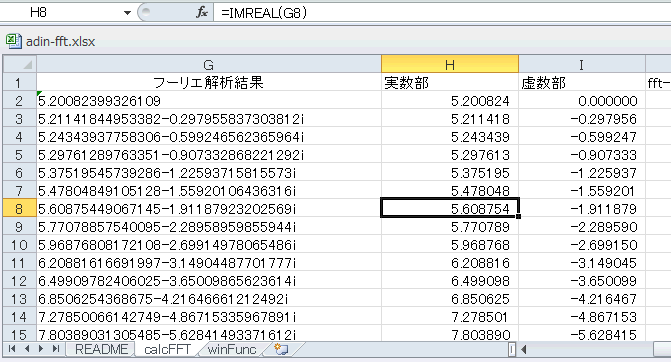
図4-33 IMREAL/IMAGINARY関数で実数/虚数を取り出す
●fft-freq列は周波数軸の計算
J列は周波数(図4‐34のグラフの横軸)になります。同図のようにサンプリング周波数(READMEのB4セル、44100Hz)をFFTの点数(1024)で割ったもの(約43Hz)が周波数分解能になり、このステップ上の周波数成分が計算されます。 |
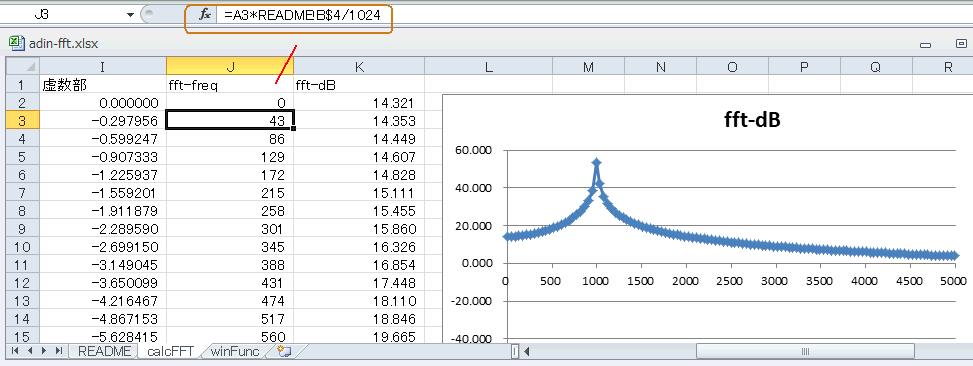
図4‐34 FFT結果のスペクトルが描かれる
●約1kHzにピークがある
K列は図4‐35のように複素数の絶対値の対数をとっています。J列が991のところの値が53.469で極大になっており、J列−K列をプロットすると図4‐34のグラフになります。 |
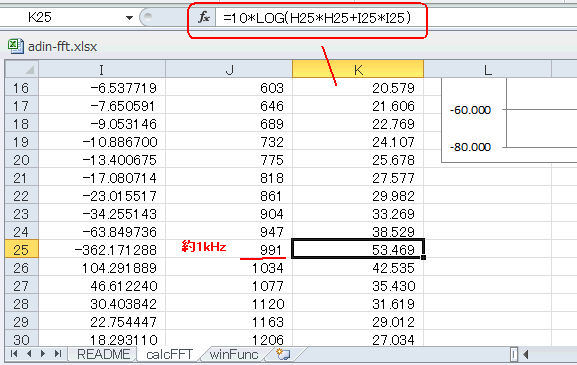
図4-35 対数をとるとグラフが見やすくなる
●もう少し複雑な信号を入力してみると…
このように1kHzのサイン波をFFTすると、その周波数のみが突出して現れます。それでは複数の周波数をミックスしてFFTするとどうなるでしょうか?(次のページ) |
次のページへ
目次へ戻る |











