7-01 LPFの係数を窓関数法で求める
本章では「窓関数法」でFIRフィルタの係数を求めます。その手順をまとめると次のようになります。
①周波数特性の決定
②逆DFTでインパルス応答を得る(*1)
③窓関数の乗算(*2)
(*1)このサイトで示すように「周波数特性の逆DFT」は「インパルス応答」に等しくなる。
(*2)その上でこのサイトのように「窓関数」を施すとリップル(波打ち)が抑えられ、良好な特性になる。 |
●こんな感じのFIRフィルタが欲しい
まずは①の周波数特性ですが、ここでは次のような仕様にします。
・サンプリング周波数: 44100Hz
・カットオフ周波数: 4000Hz
・フィルタタイプ: 低域通過型(LPF)
・タップ数(次数、係数の数): 140
●FIRフィルタを設計するEXCELファイル
このEXCELをダウンロードして開きます。最初のREADMEシート(図7‐01)に示すように、各シートの計算にはVBAを使用します。 |
図7-01 計算は基本的にVBAで
| 「開発タブ」からVisual Basicをクリックし、Module01を開きます(図7‐02)。これは「周波数特性」を与えるVBAマクロになります。実行(三角マーク)をクリックしましょう。 |
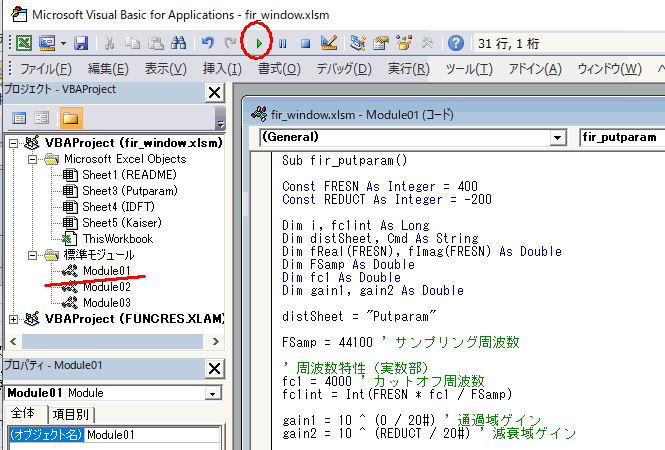
図7-02 Module01にサンプリングやカットオフ周波数がある
●このLPF特性が目標になる
Putparamシートを見ると、図7‐03のようなグラフが描かれています。fReal[i]は400点あり、200点目がナイキスト周波数、400点目がサンプリング周波数に相当します(*3)。離散信号の周波数特性はナイキストを中心に対称になることを鑑みると、これは「低域通過特性」になります。
(*3)fReal[i]の"i"の間隔は44100/400 = 110.25Hz、それに"i"をかけたものがその点の周波数になる。 |
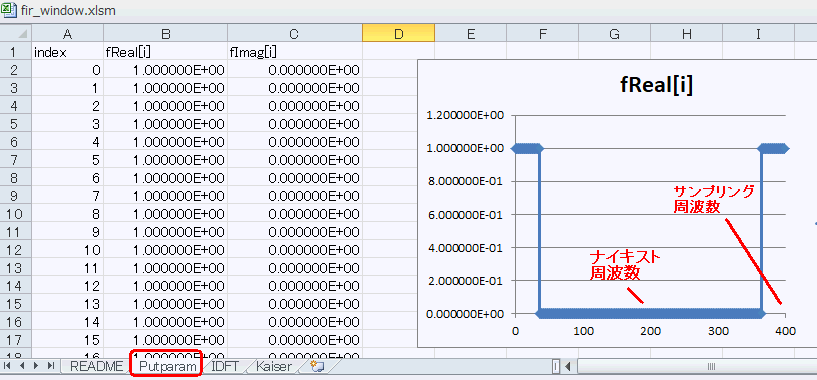
図7-03 周波数特性の実数部
●振幅特性だけ与えて位相特性は与えない
fRealの下にfImagのグラフがあります。周波数特性は複素数で表されますが、このように虚数部は常に0とします(*4)。
(*4)「振幅特性」は複素数の絶対値なのでfRealと等しくなり、「位相特性」は複素数の角度なので常に0度になる |
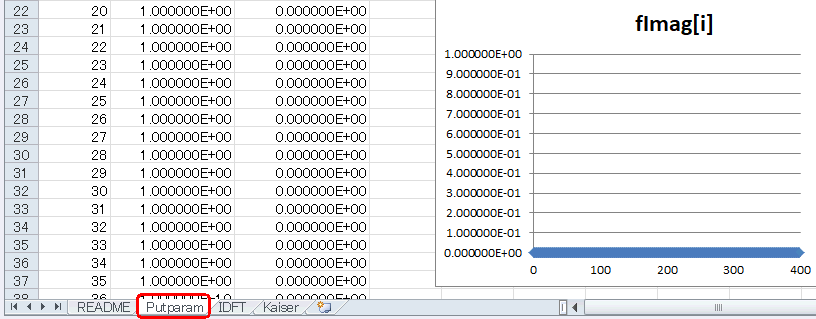
図7‐04 周波数特性の虚数部
●IDFT (Inverse Discrete Fourier Transform)
次は②逆DFTでインパルス応答です。図7‐05のようにModule02を開きます。これは上記の周波数特性を読み込んで逆DFTするVBAマクロです。 |
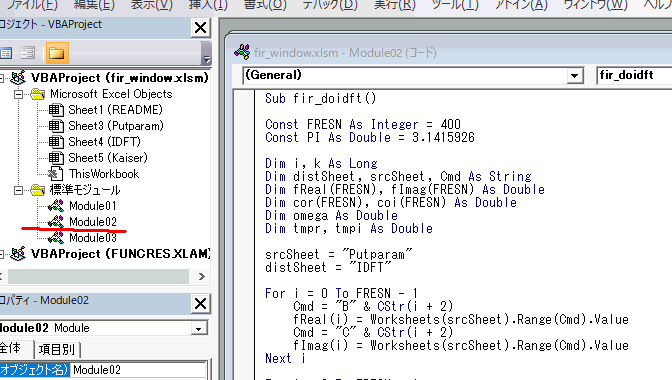
図7‐05 Module02に逆DFTのプログラム
●周波数特性の逆DFTはインパルス応答
Module02を実行すると図7‐06のようにIDFTシートにグラフが現れます。coReal[i]がインパルス応答になります(データ数は400)。 |
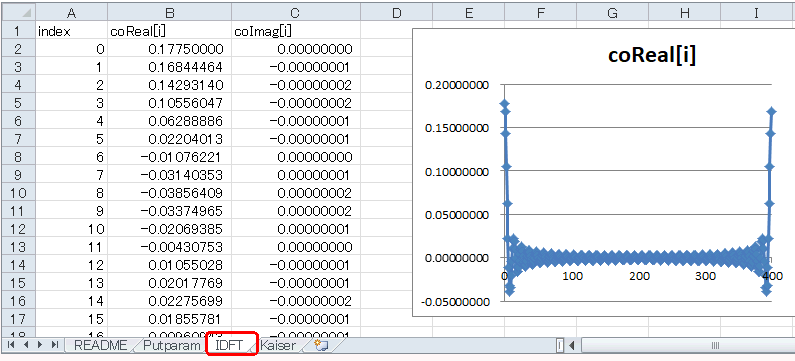
図7‐06 逆DFTの結果(実数部)
その下にcoImag[i]のグラフがありますが、このように皆0になります(*5)。
(*5)図7‐03のような左右対称なデータ列をDFTすると虚数部はほぼ0になる(図7-07のC列) |
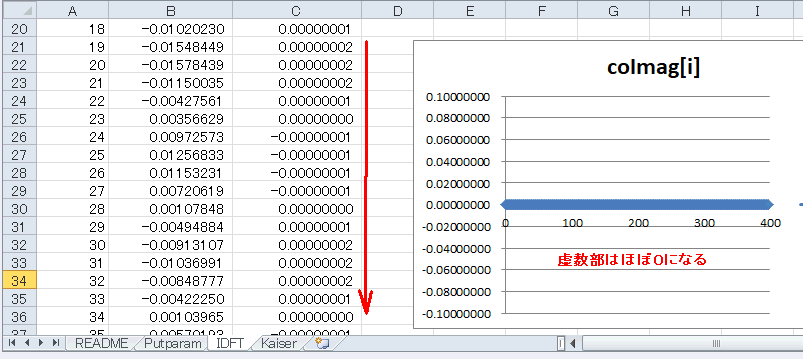
図7‐07 逆DFTの結果(虚数部)
次のページへ
目次へ戻る |













