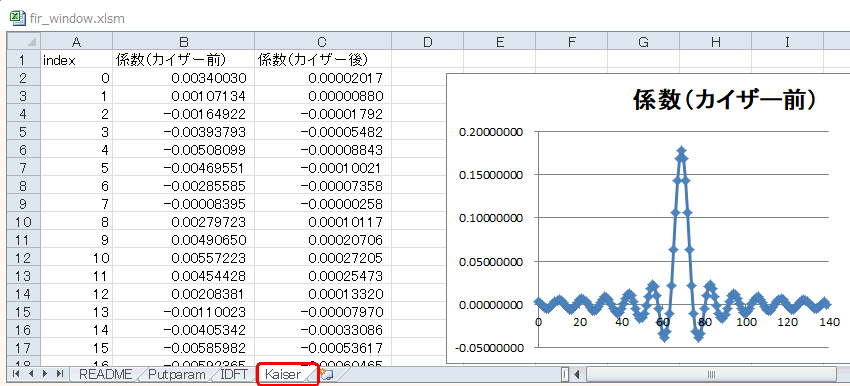
7-01　LPFの係数を窓関数法で求める（続き） 　最後に�B窓関数の乗算ですが、図7‐10のようにModule03を開きます。これは「インパルス応答の並び替え（＊１）」と「カイザー窓（＊２）」を施すVBAマクロです。 （＊１）このサイトの「インパルス応答のシフト」参照。 （＊２）このサイトの下の方にカイザー窓の説明。 　　図7-10　Module03に窓関数がある ●窓関数を施す前と後の係数 　Module03を実行するとKaiserシートに係数が現れます。「カイザー前」は逆DFT結果を並び替えたもので、図7‐11のように140タップ、左右対称になります（＊３）。 （＊３）逆DFT結果は400点あるが、その中の140点をとって並び替え。詳しくはModule03を参照 　　図7-11　これは窓関数前 　その下の「カイザー後」のグラフはカイザー窓を施した後の係数になります（図7‐12）。上図と比較すると係数の前方と後方のリップルが抑えられています。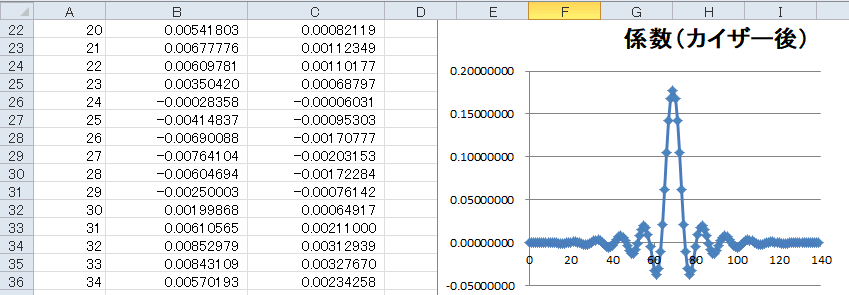 　　図7-12　これは窓関数の後 ●別のEXCELでF特の計算をしてみる 　得られた係数を使って周波数特性を見てみましょう。このサイトからFIR特性計算用EXCELをダウンロードして開きます。B列の係数を140個コピーして firnorm-fres-io.xlsm のf-responseシートD列にペーストします。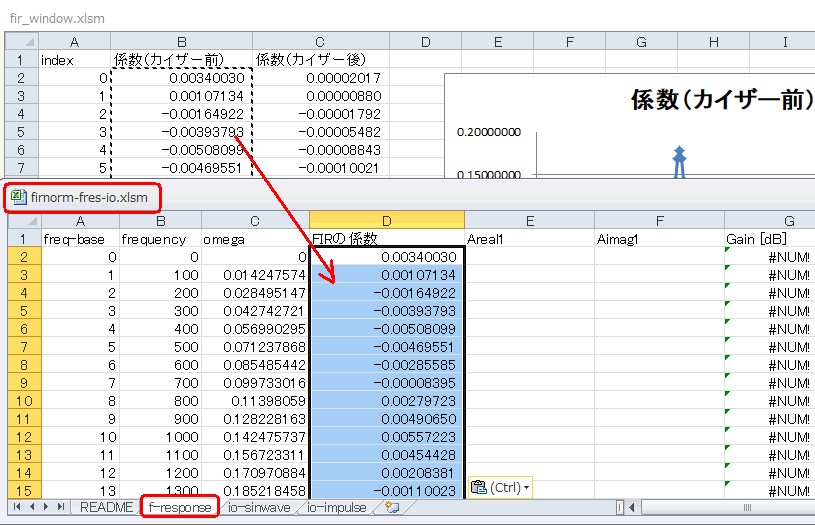 　　図7-13　EXCELファイルをまたいだコピペ。GainやThetaはVBAで計算 ●F特もVBAで計算させる 　周波数特性を計算するにはVBA (Module1)を実行する必要があります。f-responseシートの右の方のグラフを見てみましょう。このように4000Hz辺りから減衰するLPFになっています。これは「カイザー前」の係数の特性です。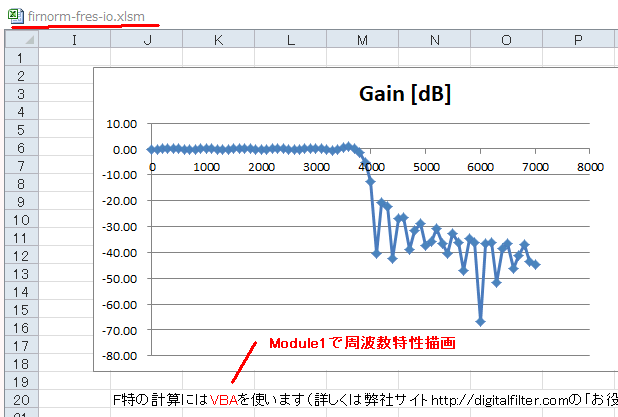 　　図7‐14　firnorm-fres-io.xlsmのModule1を実行する ●窓関数の効果を確認しよう 　それでは「カイザー後」の係数をコピペしてみましょう。すると図7‐15のようにカットオフが急峻になり、減衰率もぐっと下がります。また通過域のリップルも抑えられています。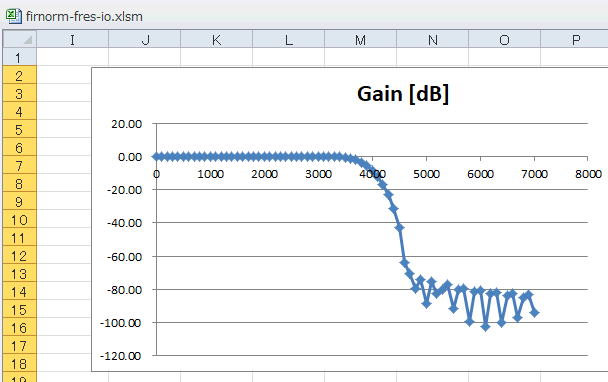 　　図7‐15　カイザー窓を施すと特性が改善！ ●フーリエ変換はFIR係数の導出にも使われる 　「インパルス応答のDFTは周波数特性」ということは「周波数特性の逆DFTはインパルス応答」になります。 　�@周波数特性の決定 　�A逆DFTでインパルス応答を得る 　そしてFIR型の場合、インパルス応答＝係数となります。さらにその後にカイザー窓を施すことにより、より性能の良い係数を得ることができます。 　�B窓関数の乗算 　以上�@�A�BのステップでFIRフィルタの係数を得ます。これを「窓関数法」といいます。 最初のページへ 目次へ戻る