6-01 バタワース型HPF(2次)を設計しよう(続き)
●あらかじめプリワーピングでカットオフ周波数をずらした理由
アナログの周波数特性は図6‐17のように無限の周波数まで続くのに対し、デジタルの周波数特性はナイキスト周波数で終わります。したがって双一次S-Z変換(後に説明)を行うと高域のアナログ周波数特性をぐっと圧縮する格好になり、それに伴いカットオフ周波数には「ずれ」が生じます。これを相殺するために、式A-02のようなプリワーピングを行い、あらかじめカットオフ周波数をずらしておくわけです。 |
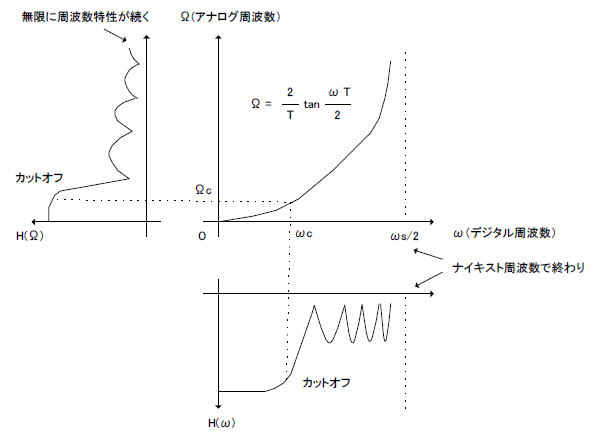
図6‐17 双一次S-Z変換による周波数特性のひずみ
■双一次S-Z変換
アナログフィルタのデジタル化には「双一次S-Z変換」を使用します。それを代表的な1次式、2次式に施して整理したものを表A-3 に示します。 |
 ★参考文献 ★参考文献
●具体的に双一次S-Z変換してみる
式5‐02のアナログHPFに表A-3を適用します。EXCELを開き、まずはα、β、G(表A-3の枠外下)を計算します。G1,
G2, G3セルをそれぞれ、
=2*44100
=E3*G1^2
=1/(G1^2+E1*G1+E2)
として計算し、右のセルにそれぞれα、β、Gと書き込みます(図6‐18)。 |
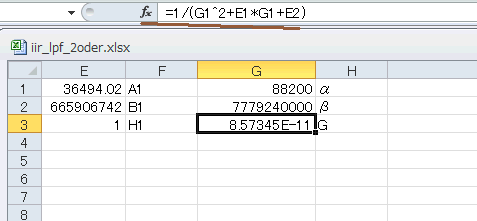
図6-18 α、β、Gの計算
次に表A-3の右下枠の部分を計算します。I1~I5セルをそれぞれ、
=G2+0*G1+0
=2*(0-G2)
=G2-0*G1+0
=2*G3*(E2-G1^2)
=G3*(G1^2-E1*G1+E2)
として計算し、右のセルにそれぞれ p_a0, p_a1, p_a2, p_b1, p_b2 と書いておきます(図6‐19)。 |
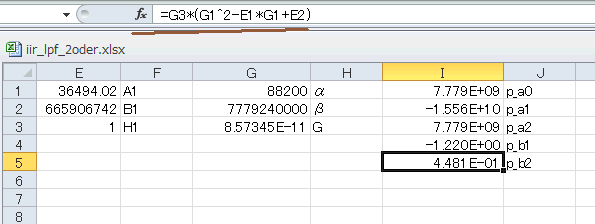
図6-19 Biquad係数の計算
| 上図の結果を表A-3の右下枠に適用すると式5‐03のような2次IIR(Biquad)の伝達関数になります。 |
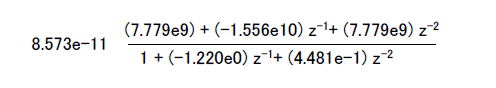 式5‐03 S-Z変換の結果 式5‐03 S-Z変換の結果
式5‐03を整理するためにK1~K5セルをそれぞれ、
=G3*I1
=G3*I2
=G3*I3
=I4
=I5
とします(分子の係数×G3、分母はそのまま)。右のセルにそれぞれa0, a1, a2, b1, b2と書き込みましょう(図6‐20)。 |
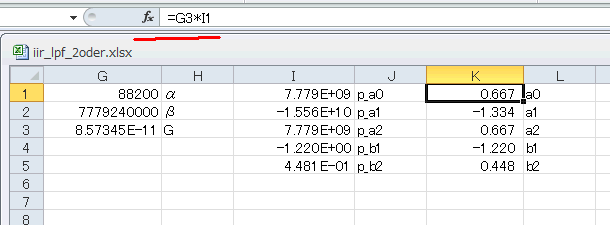
図6-20 Biquadの係数を整理する
| するとBiquadの伝達関数は式5‐04のようになります。 |
 式5‐04 2次IIRフィルタの伝達関数 式5‐04 2次IIRフィルタの伝達関数
●カットオフ周波数などの確認
Biquadの周波数特性を見てみましょう。このサイトからEXCELをダウンロードして開き、f-responseシートを開きます。D列に上式の係数をペーストします(これ)。 |

図6‐22 Biquadの周波数特性を計算するEXCEL
f-responseシートの右端に周波数特性があります。4000Hzで-3dBになっており、正しくS-Z変換されていることが分かります(*1)。
(*1)アナログフィルタではカットオフをあえて4000Hz→4111Hzとずらした。S-Z変換によってそのずれが相殺される。 |
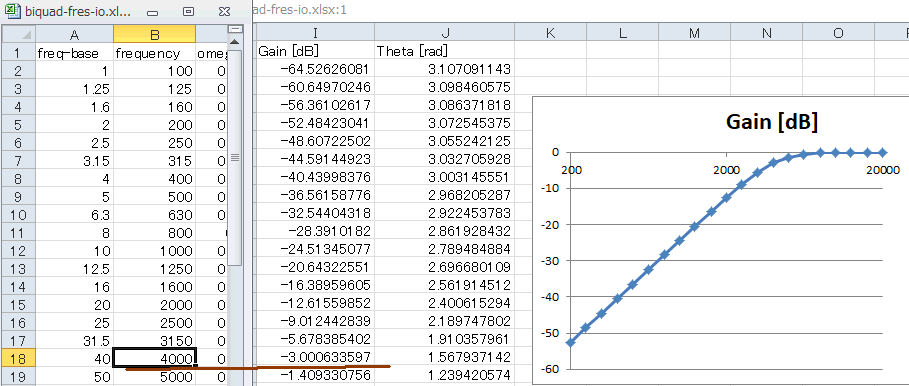
図6‐23 4000Hzで-3dBになっている。F特計算開始周波数(READMEシートのB6セル)など適当に変更
以上でバタワース型IIRフィルタ(2次)の設計は終了です。
①アナログ基準LPF
②プリワーピング
③周波数変換
④双一次S-Z変換
このような順序で進めます。LPF/HPF/BPR/BRFにかかわらず、①はアナログ基準"LPF"であることに注意しましょう。
★参考文献
以下の文献から引用。
「ディジタル・フィルタ設計入門」、尾知博、CQ出版社、1990年
「実践ディジタル・フィルタ設計入門」、岩田利王、CQ出版社、2004年 |
最初のページへ
目次へ戻る |

 ★参考文献
★参考文献

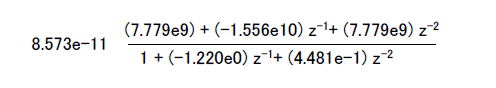 式5‐03 S-Z変換の結果
式5‐03 S-Z変換の結果
 式5‐04 2次IIRフィルタの伝達関数
式5‐04 2次IIRフィルタの伝達関数
