6-02 チェビシェフ型HPF(2次)を設計しよう(続き)
■双一次S-Z変換
アナログフィルタのデジタル化には「双一次S-Z変換」を使用します。それを代表的な1次式、2次式に施して整理したものを表A-3 に示します。 |
 ★参考文献 ★参考文献
●具体的に双一次S-Z変換してみる
式5‐12のアナログHPFに表A-3を適用します。EXCELを開き、まずはα、β、G(表A-3の枠外下)を計算します。G1,
G2, G3セルをそれぞれ、
=2*44100
=E3*G1^2
=1/(G1^2+E1*G1+E2)
として計算し、右のセルにそれぞれα、β、Gと書き込みます(図6‐48)。 |
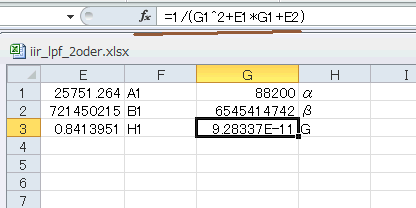
図6-48 α、β、Gの計算
次に表A-3の右下枠の部分を計算します。I1〜I5セルをそれぞれ、
=G2+0*G1+0
=2*(0-G2)
=G2-0*G1+0
=2*G3*(E2-G1^2)
=G3*(G1^2-E1*G1+E2)
として計算し、右のセルにそれぞれ p_a0, p_a1, p_a2, p_b1, p_b2 と書いておきます(図6‐49)。 |
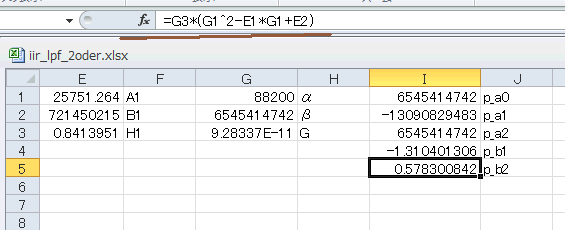
図6-49 Biquad係数の計算
| 上図の結果を表A-3の右下枠に適用すると式5‐13のような2次IIR(Biquad)の伝達関数になります。 |
 式5‐13 S-Z変換の結果 式5‐13 S-Z変換の結果
式5‐13を整理するためにK1〜K5セルをそれぞれ、
=G3*I1
=G3*I2
=G3*I3
=I4
=I5
とします(分子の係数×G3、分母はそのまま)。右のセルにそれぞれa0, a1, a2, b1, b2と書き込みましょう(図6-50)。 |

図6-50 Biquadの係数を整理する
| するとBiquadの伝達関数は式5‐14のようになります。 |
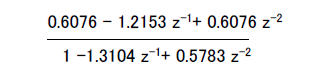 式5‐14 2次IIRフィルタの伝達関数 式5‐14 2次IIRフィルタの伝達関数
●カットオフ周波数などの確認
Biquadの周波数特性を見てみましょう。このサイトからEXCELをダウンロードして開き、f-responseシートを開きます。D列に上式の係数をペーストします(これ)。 |
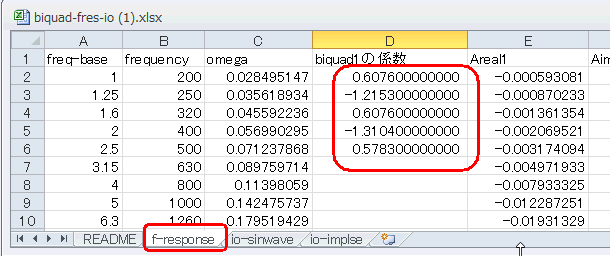
図6-52 Biquadの周波数特性を計算するEXCEL
f-responseシートの右端に周波数特性があります。4000Hzで-1.5dBになっており、正しくS-Z変換されていることが分かります(*1)。
(*1)アナログフィルタではカットオフをあえて4000Hz→4111Hzとずらした。S-Z変換によってそのずれが相殺される。 |
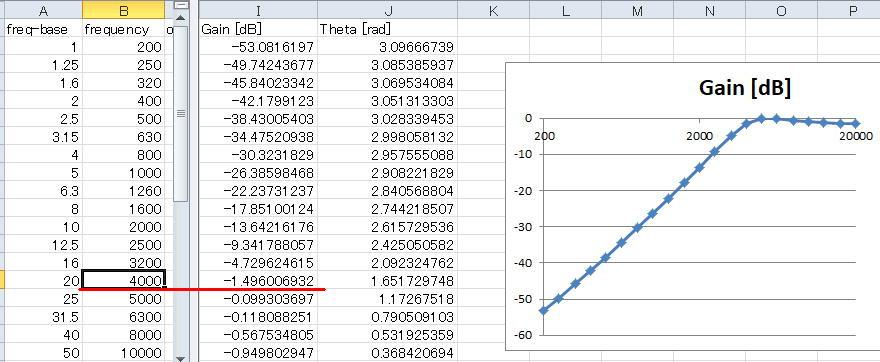
図6-53 4000Hzで-1.5dBになっている。F特計算開始周波数(READMEシートのB6セル)など適当に変更
バタワース型と比較すると、チェビシェフ型は通過域と減衰域の切り替わりにメリハリが効いており、代わりに通過域にリップル(上図では1.5dB)を持っています。
チェビシェフ型IIRフィルタ(2次)の設計はまとめると以下のようになります。
①アナログ基準LPF
②プリワーピング
③周波数変換
④双一次S-Z変換
バタワース型との違いは、①のアナログ基準LPFだけになります。「通過/減衰のメリハリ」と「通過域のリップル」のトレードオフを鑑みて使い分けましょう。
★参考文献
以下の文献から引用。
「ディジタル・フィルタ設計入門」、尾知博、CQ出版社、1990年
「実践ディジタル・フィルタ設計入門」、岩田利王、CQ出版社、2004年 |
最初のページへ
目次へ戻る |
 ★参考文献
★参考文献

 式5‐13 S-Z変換の結果
式5‐13 S-Z変換の結果
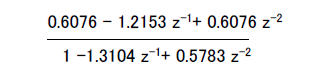 式5‐14 2次IIRフィルタの伝達関数
式5‐14 2次IIRフィルタの伝達関数

 ★参考文献
★参考文献

 式5‐13 S-Z変換の結果
式5‐13 S-Z変換の結果
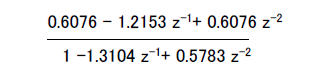 式5‐14 2次IIRフィルタの伝達関数
式5‐14 2次IIRフィルタの伝達関数
